Točno
8. prosinca 2013. 12:04 (11 godine, 3 mjeseci)
Sakrij rješenje
Zadana je uređena trojka brojeva
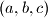
na kojoj možemo vršiti sljedeću operaciju: uzmemo dva broja iz trojke i zamijenimo ih s
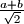
i
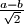
. Možemo li doći do trojke
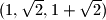
krenuvši od trojke
?
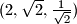
%V0
Zadana je uređena trojka brojeva $(a, b, c)$ na kojoj možemo vršiti sljedeću operaciju: uzmemo dva broja iz trojke i zamijenimo ih s $\frac{a+b}{\sqrt{2}}$ i $\frac{a-b}{\sqrt{2}}$. Možemo li doći do trojke $(1, \sqrt{2}, 1 + \sqrt{2})$ krenuvši od trojke $(2, \sqrt{2}, \frac{1}{\sqrt{2}})$?
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Rjesenje: Ne, zato sto je
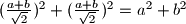
pa je zbroj kvadrata elemenata invarijantan.
%V0
Rjesenje: Ne, zato sto je $(\frac{a+b}{\sqrt{2}})^2+(\frac{a+b}{\sqrt{2}})^2 = a^2 + b^2$ pa je zbroj kvadrata elemenata invarijantan.
| 10. prosinca 2013. 14:27 | ikicic | Točno |
Školjka