Neocijenjeno
8. prosinca 2013. 12:05 (10 godine, 5 mjeseci)
Sakrij rješenje
U trokutu
simetrale kuta
pri vrhu
siječe nasuprotnu stranicu
u točki
. Točka
izvan trokuta
je takva da je
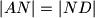
i da je
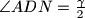
. Dokažite da je
simetrala kuta
.
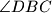
%V0
U trokutu $ABC$ simetrale kuta $\gamma$ pri vrhu $C$ siječe nasuprotnu stranicu $\overline{AB}$ u točki $N$. Točka $D$ izvan trokuta $ABC$ je takva da je $|AN|=|ND|$ i da je $\angle{ADN}= \frac{\gamma}{2}$. Dokažite da je $AB$ simetrala kuta $\angle{DBC}$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Trokut
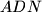
je jednakokračan pa je
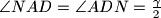
. Budući da je
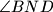
vanjski kut tog trokuta vrijedi
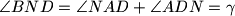
. Po teoremu o simetrali kuta vrijedi
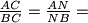
(po uvijetu zadatka)
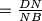
. Po teoremu SKS zakljucujemo da su trokuti
i
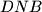
slični. Zato je
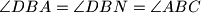
odnosno polupravac
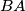
dijeli kut
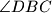
na dva jednaka dijela, pa je simetrala.
%V0
Trokut $ADN$ je jednakokračan pa je $\angle{NAD} = \angle{ADN} = \frac{\gamma}{2}$. Budući da je $\angle{BND}$ vanjski kut tog trokuta vrijedi $ \angle{BND} = \angle{NAD} + \angle{ADN} = \gamma $. Po teoremu o simetrali kuta vrijedi $ \frac{AC}{BC} = \frac{AN}{NB}=$ (po uvijetu zadatka) $=\frac{DN}{NB}$. Po teoremu SKS zakljucujemo da su trokuti $ABC$ i $DNB$ slični. Zato je $\angle{DBA} = \angle{DBN} = \angle{ABC}$ odnosno polupravac $BA$ dijeli kut $\angle{DBC}$ na dva jednaka dijela, pa je simetrala.
Školjka