Točno
8. prosinca 2013. 12:07 (12 godine, 1 mjesec)
Sakrij rješenje
Dokaži da za svaki prost broj

vrijedi. Ako
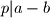
onda
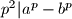
%V0
Dokaži da za svaki prost broj $p$ vrijedi. Ako $p|a-b$ onda $p^2|a^p - b^p$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Raspises razliku

-tih potencija,

je djeljivo s

. Dakle, dovoljno je pokazati da je
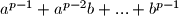
djeljivo s

. Ako uvrstimo da je
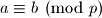
dobivamo da je
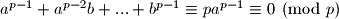
%V0
Raspises razliku $p$-tih potencija, $a-b$ je djeljivo s $p$. Dakle, dovoljno je pokazati da je $a^{p-1} + a^{p-2}b + ... + b^{p-1}$ djeljivo s $p$. Ako uvrstimo da je $a \equiv b \pmod p$ dobivamo da je $a^{p-1} + a^{p-2}b + ... + b^{p-1} \equiv pa^{p-1} \equiv 0 \pmod p$
| 10. prosinca 2013. 19:58 | ikicic | Točno |