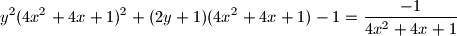Točno
8. prosinca 2013. 16:15 (12 godine, 1 mjesec)
Sakrij rješenje
Sakrij rješenje
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
supstituiramo 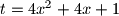 , primjetimo da je tada i
, primjetimo da je tada i 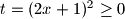 , te zbog uvjeta zadatka znamo da
, te zbog uvjeta zadatka znamo da 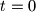 nije rjesenje. Mnozenjem s
nije rjesenje. Mnozenjem s  , i grupiranjem za kvadratnu po
, i grupiranjem za kvadratnu po  slijedi:
slijedi:
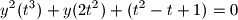
diskriminantna ove jednadbe mora biti nenegativna buduci da trazimo realne , dakle mora biti
, dakle mora biti
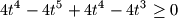
to jest
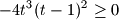
zbog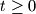 ovo je moguce jedino kad je
ovo je moguce jedino kad je 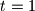 . tada je
. tada je 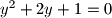 , tj
, tj 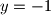 , te
, te 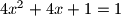 , tj
, tj 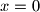 ili
ili 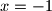 .
.
sve u svemu, imamo rjesenja,
rjesenja, 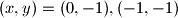 .
.
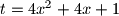 , primjetimo da je tada i
, primjetimo da je tada i 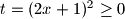 , te zbog uvjeta zadatka znamo da
, te zbog uvjeta zadatka znamo da 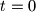 nije rjesenje. Mnozenjem s
nije rjesenje. Mnozenjem s  , i grupiranjem za kvadratnu po
, i grupiranjem za kvadratnu po  slijedi:
slijedi: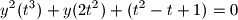
diskriminantna ove jednadbe mora biti nenegativna buduci da trazimo realne
 , dakle mora biti
, dakle mora biti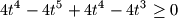
to jest
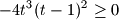
zbog
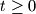 ovo je moguce jedino kad je
ovo je moguce jedino kad je 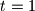 . tada je
. tada je 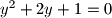 , tj
, tj 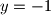 , te
, te 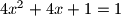 , tj
, tj 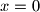 ili
ili 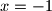 .
.sve u svemu, imamo
 rjesenja,
rjesenja, 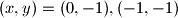 .
.  Školjka
Školjka 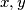 za koje vrijedi
za koje vrijedi