Točno
8. prosinca 2013. 12:08 (10 godine, 5 mjeseci)
Sakrij rješenje
Koliko ima
-članih podskupova skupa
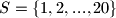
od kojih ni jedan ne sadrži
uzastopna broja?
%V0
Koliko ima $3$-članih podskupova skupa $S=\{1, 2, ..., 20\}$ od kojih ni jedan ne sadrži $2$ uzastopna broja?
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Rjesenje: Uzmemo sve troclane i oduzmemo one koji imaju uzastopne, pa dodamo nazad one koje imaju 3 uzastopna.
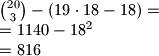
%V0
Rjesenje: Uzmemo sve troclane i oduzmemo one koji imaju uzastopne, pa dodamo nazad one koje imaju 3 uzastopna.
${20 \choose 3} - (19 \cdot 18 - 18)=\\ =1140-18^2\\=816$
| 10. prosinca 2013. 19:58 | ikicic | Točno |
Školjka