Neocijenjeno
8. prosinca 2013. 12:09 (12 godine, 1 mjesec)
Sakrij rješenje
Sakrij rješenje
Zadane su 2 kružnice,  i
i  , koje se sijeku u točkama
, koje se sijeku u točkama  i
i  . Neka je
. Neka je  pravac određen točkama
pravac određen točkama  i
i  . Dane su proizvoljne točke
. Dane su proizvoljne točke  i
i  s pravca
s pravca  tako da je dužina
tako da je dužina 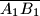 sadržana u dužini
sadržana u dužini  , te tako da vrijedi
, te tako da vrijedi 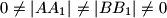 . Na kružnici
. Na kružnici  , odabrane su točke
, odabrane su točke  i
i  , s iste strane pravca
, s iste strane pravca  , takve da su pravci
, takve da su pravci 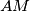 i
i 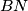 tangente na kružnicu
tangente na kružnicu  . Na kružnici
. Na kružnici  , odabrane su točke
, odabrane su točke  i
i  , s iste strane pravca
, s iste strane pravca  , ali s različite strane u odnosu na točke
, ali s različite strane u odnosu na točke  i
i  , takve da su pravci
, takve da su pravci 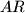 i
i  tangente na kružnicu
tangente na kružnicu  . Dokažite da se pravci
. Dokažite da se pravci  i
i 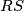 sijeku u točki koja je na pravcu
sijeku u točki koja je na pravcu  .
.
 i
i  , koje se sijeku u točkama
, koje se sijeku u točkama  i
i  . Neka je
. Neka je  pravac određen točkama
pravac određen točkama  i
i  . Dane su proizvoljne točke
. Dane su proizvoljne točke  i
i  s pravca
s pravca  tako da je dužina
tako da je dužina 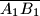 sadržana u dužini
sadržana u dužini  , te tako da vrijedi
, te tako da vrijedi 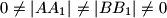 . Na kružnici
. Na kružnici  , odabrane su točke
, odabrane su točke  i
i  , s iste strane pravca
, s iste strane pravca  , takve da su pravci
, takve da su pravci 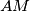 i
i 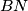 tangente na kružnicu
tangente na kružnicu  . Na kružnici
. Na kružnici  , odabrane su točke
, odabrane su točke  i
i  , s iste strane pravca
, s iste strane pravca  , ali s različite strane u odnosu na točke
, ali s različite strane u odnosu na točke  i
i  , takve da su pravci
, takve da su pravci 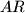 i
i  tangente na kružnicu
tangente na kružnicu  . Dokažite da se pravci
. Dokažite da se pravci  i
i 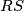 sijeku u točki koja je na pravcu
sijeku u točki koja je na pravcu  .
. Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
neka je  sjeciste od
sjeciste od 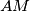 i
i 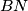 , te neka je
, te neka je  sjeciste
sjeciste  i
i  , jasno ova dva pravca nisu paralelna zbog uvjeta
, jasno ova dva pravca nisu paralelna zbog uvjeta 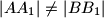 . menelaj na trokut
. menelaj na trokut  s obzirom na pravac
s obzirom na pravac  nam daje
nam daje
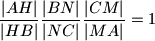
kako je ocito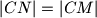 , slijedi
, slijedi
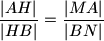
ista prica sa druge strane, uz sjeciste
sjeciste 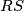 i
i  daje
daje
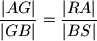
ali potencija tocke nam daje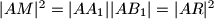 , te
, te 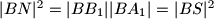 , sto nam daje
, sto nam daje
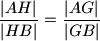
sto znaci da i
i  dijele
dijele  u istom omjeru, a buduci da su te dvije tocke s istih strana tocaka i
u istom omjeru, a buduci da su te dvije tocke s istih strana tocaka i  i
i  , zakljucujemo da su one medusobno jednake, iz cega slijedi tvrdnja zadatka.
, zakljucujemo da su one medusobno jednake, iz cega slijedi tvrdnja zadatka.
 sjeciste od
sjeciste od 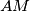 i
i 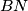 , te neka je
, te neka je  sjeciste
sjeciste  i
i  , jasno ova dva pravca nisu paralelna zbog uvjeta
, jasno ova dva pravca nisu paralelna zbog uvjeta 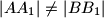 . menelaj na trokut
. menelaj na trokut  s obzirom na pravac
s obzirom na pravac  nam daje
nam daje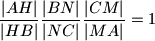
kako je ocito
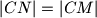 , slijedi
, slijedi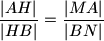
ista prica sa druge strane, uz
 sjeciste
sjeciste 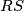 i
i  daje
daje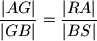
ali potencija tocke nam daje
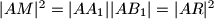 , te
, te 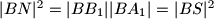 , sto nam daje
, sto nam daje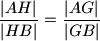
sto znaci da
 i
i  dijele
dijele  u istom omjeru, a buduci da su te dvije tocke s istih strana tocaka i
u istom omjeru, a buduci da su te dvije tocke s istih strana tocaka i  i
i  , zakljucujemo da su one medusobno jednake, iz cega slijedi tvrdnja zadatka.
, zakljucujemo da su one medusobno jednake, iz cega slijedi tvrdnja zadatka.  Školjka
Školjka