Neocijenjeno
8. prosinca 2013. 12:11 (10 godine, 11 mjeseci)
Sakrij rješenje
Za
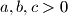
dokaži da vrijedi:
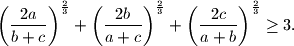
%V0
Za $a,b,c>0$ dokaži da vrijedi: $$\left( \frac{2a}{b+c} \right)^{\frac{2}{3}}+\left( \frac{2b}{a+c} \right)^{\frac{2}{3}}+\left( \frac{2c}{a+b} \right)^{\frac{2}{3}} \geq 3 \text{.}$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Iz AG nejednakost imamo:
![\sum \left( \frac{2a}{b+c} \right)^{\frac{2}{3}} = \sum \frac{2a}{\sqrt[3]{2a(b+c)^2}} \ge \sum \frac{2a}{\frac{1}{3}(2a+2(b+c))} =3](/media/m/9/0/e/90e52dcbf5bf9632cc1f15d492dba044.png)
%V0
Iz AG nejednakost imamo:
$\sum \left( \frac{2a}{b+c} \right)^{\frac{2}{3}} = \sum \frac{2a}{\sqrt[3]{2a(b+c)^2}} \ge \sum \frac{2a}{\frac{1}{3}(2a+2(b+c))} =3$
Školjka