Neocijenjeno
8. prosinca 2013. 17:17 (12 godine, 1 mjesec)
Sakrij rješenje
Sakrij rješenje
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
dokazat cemo cak nesto jacu tvrdnju:
Neka su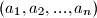 cijeli brojevi. Tada postoje cijeli brojevi
cijeli brojevi. Tada postoje cijeli brojevi 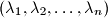 , koji su svi razliciti od
, koji su svi razliciti od  , takvi da je
, takvi da je 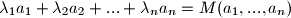
za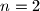 , ovo je poznata lema. za slucaj da netko nezna lemu, evo leme i dokaza:
, ovo je poznata lema. za slucaj da netko nezna lemu, evo leme i dokaza:
lema neka su i
i  cijeli brojevi. tada postoje cijeli brojevi
cijeli brojevi. tada postoje cijeli brojevi  i
i  takvi da je
takvi da je 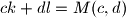
dokaz neka je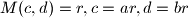 . promotrimo brojeve
. promotrimo brojeve 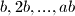 . u ovome skupu od
. u ovome skupu od  brojeva, pojavljuju se svi moguci ostaci modulo
brojeva, pojavljuju se svi moguci ostaci modulo  . zaista kada nebi bilo tako, onda se neki ostatak nebi pojavljivao, pa bi se nuzno neki ostatak morao javiti dva puta. drugim rjecima, bilo bi
. zaista kada nebi bilo tako, onda se neki ostatak nebi pojavljivao, pa bi se nuzno neki ostatak morao javiti dva puta. drugim rjecima, bilo bi 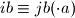 , za neke razlicite
, za neke razlicite  i
i  iz skupa
iz skupa 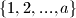 . ali tada bi bilo
. ali tada bi bilo 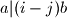 . no zbog toga sto su
. no zbog toga sto su  i
i  po pretpostavci relativno prosti, znacilo bi da
po pretpostavci relativno prosti, znacilo bi da 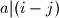 , sto ocito nije moguce s obzirom da su
, sto ocito nije moguce s obzirom da su  i
i  iz skupa
iz skupa 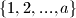 , pa je njihova razlika po apsolutnoj vrijednosti manja od
, pa je njihova razlika po apsolutnoj vrijednosti manja od  . dakle, medu pocetnih
. dakle, medu pocetnih  brojeva
brojeva 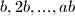 , javljaju se svi moguci ostaci modulo
, javljaju se svi moguci ostaci modulo  , pa tako posebno i ostatak
, pa tako posebno i ostatak  . neka je onda
. neka je onda 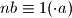 . drugim rjecima, postoji cijeli broj
. drugim rjecima, postoji cijeli broj  tako da je
tako da je 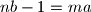 , tj
, tj 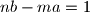 . uz
. uz 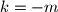 i
i 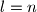 , pronasli smo
, pronasli smo  i
i  koji zadovoljavaju
koji zadovoljavaju 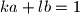 , tj mnozeci s
, tj mnozeci s  ,
, 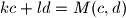 , cime je lema dokazana.
, cime je lema dokazana.
dodatno, za potrebe naseg zadatka, postoje takvi i
i  koji su oba razliti od
koji su oba razliti od  . zaista, cim su i
. zaista, cim su i  i
i  razliciti od
razliciti od  , jasno je da nece ni
, jasno je da nece ni  ni
ni  biti jednaki
biti jednaki  , jer u suprotnom bismo imali npr
, jer u suprotnom bismo imali npr 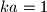 , za
, za 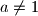 , sto naravno ne moze vrijediti. s druge strane, ako je tocno jedan od brojeva, npr
, sto naravno ne moze vrijediti. s druge strane, ako je tocno jedan od brojeva, npr  jednak
jednak  , lako se uzme
, lako se uzme 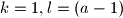 . naposlijetku, ako su oba jednaka
. naposlijetku, ako su oba jednaka  , naravno, uzme se
, naravno, uzme se 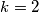 ,
, 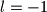 , pa tvrdnja ponovo vrijedi.
, pa tvrdnja ponovo vrijedi.
nastavljamo s dokazom koristeci indukciju. baza, za , tvrdnja vrijedi. pretpostavimo da vrijedi za broj
, tvrdnja vrijedi. pretpostavimo da vrijedi za broj  , te dokazimo da vrijedi za
, te dokazimo da vrijedi za  . kako vrijedi za
. kako vrijedi za  , pronadimo brojeve
, pronadimo brojeve  , takve da je
, takve da je 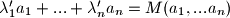 . ali sada ponovo upotrijebimo tvrdnju za
. ali sada ponovo upotrijebimo tvrdnju za  i brojeve
i brojeve 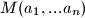 i broj
i broj 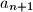 . drugim rjecima, postoje
. drugim rjecima, postoje  i
i  , oba razliciti od
, oba razliciti od  takvi da je
takvi da je 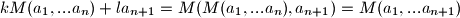 . dakle nasa tvrdnja vrijedi uz
. dakle nasa tvrdnja vrijedi uz 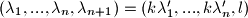 , te je jasno da su svi ovi brojevi razlicti od
, te je jasno da su svi ovi brojevi razlicti od  .
.
posebno, za ovaj zadatak znamo da je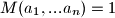 , dakle, postoje
, dakle, postoje 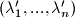 za koje vrijedi
za koje vrijedi 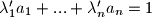 , pa za
, pa za 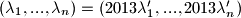 vrijedi tvrdnja zadatka.
vrijedi tvrdnja zadatka.
Neka su
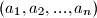 cijeli brojevi. Tada postoje cijeli brojevi
cijeli brojevi. Tada postoje cijeli brojevi 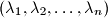 , koji su svi razliciti od
, koji su svi razliciti od  , takvi da je
, takvi da je 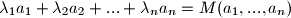
za
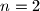 , ovo je poznata lema. za slucaj da netko nezna lemu, evo leme i dokaza:
, ovo je poznata lema. za slucaj da netko nezna lemu, evo leme i dokaza:lema neka su
 i
i  cijeli brojevi. tada postoje cijeli brojevi
cijeli brojevi. tada postoje cijeli brojevi  i
i  takvi da je
takvi da je 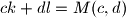
dokaz neka je
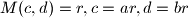 . promotrimo brojeve
. promotrimo brojeve 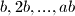 . u ovome skupu od
. u ovome skupu od  brojeva, pojavljuju se svi moguci ostaci modulo
brojeva, pojavljuju se svi moguci ostaci modulo  . zaista kada nebi bilo tako, onda se neki ostatak nebi pojavljivao, pa bi se nuzno neki ostatak morao javiti dva puta. drugim rjecima, bilo bi
. zaista kada nebi bilo tako, onda se neki ostatak nebi pojavljivao, pa bi se nuzno neki ostatak morao javiti dva puta. drugim rjecima, bilo bi 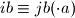 , za neke razlicite
, za neke razlicite  i
i  iz skupa
iz skupa 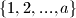 . ali tada bi bilo
. ali tada bi bilo 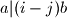 . no zbog toga sto su
. no zbog toga sto su  i
i  po pretpostavci relativno prosti, znacilo bi da
po pretpostavci relativno prosti, znacilo bi da 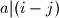 , sto ocito nije moguce s obzirom da su
, sto ocito nije moguce s obzirom da su  i
i  iz skupa
iz skupa 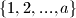 , pa je njihova razlika po apsolutnoj vrijednosti manja od
, pa je njihova razlika po apsolutnoj vrijednosti manja od  . dakle, medu pocetnih
. dakle, medu pocetnih  brojeva
brojeva 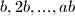 , javljaju se svi moguci ostaci modulo
, javljaju se svi moguci ostaci modulo  , pa tako posebno i ostatak
, pa tako posebno i ostatak  . neka je onda
. neka je onda 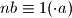 . drugim rjecima, postoji cijeli broj
. drugim rjecima, postoji cijeli broj  tako da je
tako da je 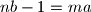 , tj
, tj 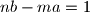 . uz
. uz 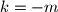 i
i 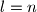 , pronasli smo
, pronasli smo  i
i  koji zadovoljavaju
koji zadovoljavaju 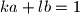 , tj mnozeci s
, tj mnozeci s  ,
, 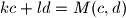 , cime je lema dokazana.
, cime je lema dokazana.dodatno, za potrebe naseg zadatka, postoje takvi
 i
i  koji su oba razliti od
koji su oba razliti od  . zaista, cim su i
. zaista, cim su i  i
i  razliciti od
razliciti od  , jasno je da nece ni
, jasno je da nece ni  ni
ni  biti jednaki
biti jednaki  , jer u suprotnom bismo imali npr
, jer u suprotnom bismo imali npr 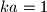 , za
, za 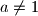 , sto naravno ne moze vrijediti. s druge strane, ako je tocno jedan od brojeva, npr
, sto naravno ne moze vrijediti. s druge strane, ako je tocno jedan od brojeva, npr  jednak
jednak  , lako se uzme
, lako se uzme 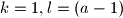 . naposlijetku, ako su oba jednaka
. naposlijetku, ako su oba jednaka  , naravno, uzme se
, naravno, uzme se 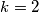 ,
, 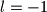 , pa tvrdnja ponovo vrijedi.
, pa tvrdnja ponovo vrijedi.nastavljamo s dokazom koristeci indukciju. baza, za
 , tvrdnja vrijedi. pretpostavimo da vrijedi za broj
, tvrdnja vrijedi. pretpostavimo da vrijedi za broj  , te dokazimo da vrijedi za
, te dokazimo da vrijedi za  . kako vrijedi za
. kako vrijedi za  , pronadimo brojeve
, pronadimo brojeve  , takve da je
, takve da je 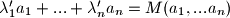 . ali sada ponovo upotrijebimo tvrdnju za
. ali sada ponovo upotrijebimo tvrdnju za  i brojeve
i brojeve 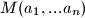 i broj
i broj 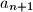 . drugim rjecima, postoje
. drugim rjecima, postoje  i
i  , oba razliciti od
, oba razliciti od  takvi da je
takvi da je 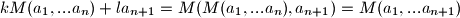 . dakle nasa tvrdnja vrijedi uz
. dakle nasa tvrdnja vrijedi uz 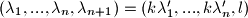 , te je jasno da su svi ovi brojevi razlicti od
, te je jasno da su svi ovi brojevi razlicti od  .
.posebno, za ovaj zadatak znamo da je
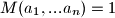 , dakle, postoje
, dakle, postoje 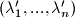 za koje vrijedi
za koje vrijedi 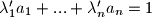 , pa za
, pa za 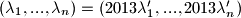 vrijedi tvrdnja zadatka.
vrijedi tvrdnja zadatka.  Školjka
Školjka 