Točno
26. ožujka 2014. 21:17 (11 godine, 10 mjeseci)
Zadana je uređena trojka brojeva
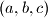
na kojoj možemo vršiti sljedeću operaciju: uzmemo dva broja iz trojke i zamijenimo ih s
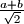
i
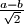
. Možemo li doći do trojke
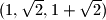
krenuvši od trojke
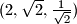
?
%V0
Zadana je uređena trojka brojeva $(a, b, c)$ na kojoj možemo vršiti sljedeću operaciju: uzmemo dva broja iz trojke i zamijenimo ih s $\frac{a+b}{\sqrt{2}}$ i $\frac{a-b}{\sqrt{2}}$. Možemo li doći do trojke $(1, \sqrt{2}, 1 + \sqrt{2})$ krenuvši od trojke $(2, \sqrt{2}, \frac{1}{\sqrt{2}})$?
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Ovo je tipičan zadatak koji možemo riješiti korištenjem invarijanti. Primjetimo da je ovdje zbir kvadrata brojeva

,

i

invarijanta. To dobijamo zbog
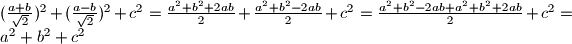
Sada zbir kvadrata za trojku
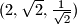
iznosi
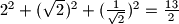
a zbir kvadrata za trojku koju treba dokučiti je
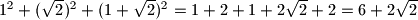
.Kako su ova dva zbira različiti slijedi da nije moguće doći nizom transformacija do date trojke pa je odgovor na pitanje zadatka ne.
%V0
Ovo je tipičan zadatak koji možemo riješiti korištenjem invarijanti. Primjetimo da je ovdje zbir kvadrata brojeva $a$,$b$ i $c$ invarijanta. To dobijamo zbog $(\frac{a+b}{\sqrt{2}})^2+(\frac{a-b}{\sqrt{2}})^2+c^2=\frac{a^2+b^2+2ab}{2}+\frac{a^2+b^2-2ab}{2}+c^2=\frac{a^2+b^2-2ab+a^2+b^2+2ab}{2}+c^2=a^2+b^2+c^2$
Sada zbir kvadrata za trojku $(2,\sqrt{2},\frac{1}{\sqrt{2}})$ iznosi $2^2+(\sqrt{2})^2+(\frac{1}{\sqrt{2}})^2=\frac{13}{{2}}$ a zbir kvadrata za trojku koju treba dokučiti je $1^2+(\sqrt{2})^2+(1+\sqrt{2})^2=1+2+1+2\sqrt{2}+2=6+2\sqrt{2}$.Kako su ova dva zbira različiti slijedi da nije moguće doći nizom transformacija do date trojke pa je odgovor na pitanje zadatka ne.
| 27. ožujka 2014. 10:52 | ikicic | Točno |
 ,
, i
i  invarijanta. To dobijamo zbog
invarijanta. To dobijamo zbog 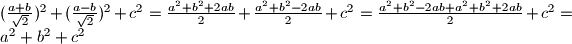
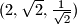 iznosi
iznosi 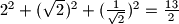 a zbir kvadrata za trojku koju treba dokučiti je
a zbir kvadrata za trojku koju treba dokučiti je 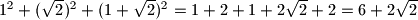 .Kako su ova dva zbira različiti slijedi da nije moguće doći nizom transformacija do date trojke pa je odgovor na pitanje zadatka ne.
.Kako su ova dva zbira različiti slijedi da nije moguće doći nizom transformacija do date trojke pa je odgovor na pitanje zadatka ne.  ,
, i
i  invarijanta. To dobijamo zbog
invarijanta. To dobijamo zbog 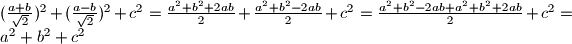
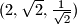 iznosi
iznosi 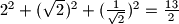 a zbir kvadrata za trojku koju treba dokučiti je
a zbir kvadrata za trojku koju treba dokučiti je 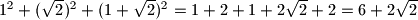 .Kako su ova dva zbira različiti slijedi da nije moguće doći nizom transformacija do date trojke pa je odgovor na pitanje zadatka ne.
.Kako su ova dva zbira različiti slijedi da nije moguće doći nizom transformacija do date trojke pa je odgovor na pitanje zadatka ne.  Školjka
Školjka 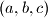 na kojoj možemo vršiti sljedeću operaciju: uzmemo dva broja iz trojke i zamijenimo ih s
na kojoj možemo vršiti sljedeću operaciju: uzmemo dva broja iz trojke i zamijenimo ih s 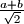 i
i 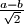 . Možemo li doći do trojke
. Možemo li doći do trojke 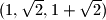 krenuvši od trojke
krenuvši od trojke 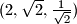 ?
?