grga, 22. travnja 2012. 19:02
EDIT
aha, monotono preuredenje vektora
a da. slijedi iz svega :)
%V0
EDIT
aha, monotono preuredenje vektora
a da. slijedi iz svega :)
grga, 22. travnja 2012. 19:01
sta je MPV nejednakost?
inace, nije neki uzas, al mozes znak mnozenja izostavljat, il ak ti bas treba, ovo se najcesce smatra prihvatljivijim
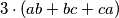
%V0
sta je MPV nejednakost?
inace, nije neki uzas, al mozes znak mnozenja izostavljat, il ak ti bas treba, ovo se najcesce smatra prihvatljivijim $3 \cdot (ab + bc + ca)$
Zadnja promjena:
grga, 22. travnja 2012. 19:01