Točno
13. travnja 2012. 17:30 (13 godine, 10 mjeseci)
Dana je trojka
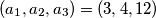
. Provodimo sljedeći postupak: biramo dva broja,

i
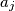
,
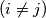
, te ih zamijenimo sa
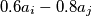
i
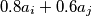
. Može li se višekratnom primjenom gore opisanog postupka dobiti trojka
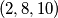
?
%V0
Dana je trojka $(a_1, a_2, a_3) = (3, 4, 12)$. Provodimo sljedeći postupak: biramo dva broja, $a_i$ i $a_j$, $(i \not= j)$, te ih zamijenimo sa $0.6a_i - 0.8a_j$ i $0.8a_i + 0.6a_j$. Može li se višekratnom primjenom gore opisanog postupka dobiti trojka $(2, 8, 10)$?
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Suma kvadrata početnih brojeva invarijanta je pri svakoj promjeni, jer je
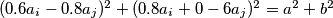
, te se stoga iz početne trojke čija je suma kvadrata jednaka 169 ne može danim postupkom doći do krajnje trojke gdje je suma kvadrata 168.
%V0
Suma kvadrata početnih brojeva invarijanta je pri svakoj promjeni, jer je $ ( 0.6a_i - 0.8a_j )^2 + ( 0.8a_i + 0-6a_j )^2 = a^2 + b^2 $, te se stoga iz početne trojke čija je suma kvadrata jednaka 169 ne može danim postupkom doći do krajnje trojke gdje je suma kvadrata 168.
| 13. travnja 2012. 17:53 | ikicic | Točno |
| 14. travnja 2012. 13:50 | grga | Točno |