Točno
19. siječnja 2014. 00:39 (12 godine)
Neka je
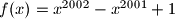
. Dokazati da su za svaki prirodan broj

brojevi

,
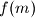
,
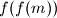
,
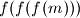
, ..., u parovima relativno prosti, tj. da nikoja dva među njima nemaju zajednički djelitelj veći od

.
%V0
Neka je $f(x) = x^{2002} - x^{2001} + 1$. Dokazati da su za svaki prirodan broj $m$ brojevi $m$, $f(m)$, $f(f(m))$, $f(f(f(m)))$, ..., u parovima relativno prosti, tj. da nikoja dva među njima nemaju zajednički djelitelj veći od $1$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Funkcija se može drugačije zapisati:
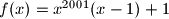
.
Označimo
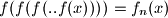
, gdje je

iterirana

puta. Definirajmo
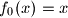
.
Dokazat ćemo indukcijom:
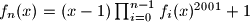
.
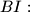
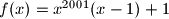
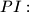
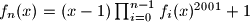
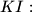
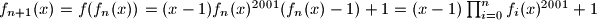
Očito je
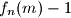
djeljivo sa svakim
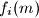
za
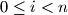
, stoga je
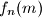
relativno prost sa svakom iteracijom od
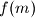
prije njega, što izravno implicira tvrdnju zadatka.
%V0
Funkcija se može drugačije zapisati: $f(x)=x^{2001}(x-1)+1$.
Označimo $f(f(f(..f(x))))=f_n(x)$, gdje je $f$ iterirana $n$ puta. Definirajmo $f_0(x)=x$.
Dokazat ćemo indukcijom: $f_n(x)=(x-1)\prod_{i=0}^{n-1}f_i(x)^{2001} + 1$.
$BI:$ $f(x)=x^{2001}(x-1)+1$
$PI:$ $f_n(x)=(x-1)\prod_{i=0}^{n-1}f_i(x)^{2001} + 1$
$KI:$ $f_{n+1}(x)=f(f_n(x))=(x-1)f_n(x)^{2001}(f_n(x) - 1) + 1=(x-1)\prod_{i=0}^{n}f_i(x)^{2001} + 1$
Očito je $f_n(m) - 1$ djeljivo sa svakim $f_i(m)$ za $0 \le i <n$, stoga je $f_n(m)$ relativno prost sa svakom iteracijom od $f(m)$ prije njega, što izravno implicira tvrdnju zadatka.
| 19. siječnja 2014. 13:51 | ikicic | Točno |