Točno
19. siječnja 2014. 13:46 (12 godine, 1 mjesec)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Neka su zacrnjeni kvadratići postavljeni i neka najmanji pravokutnik ("minimum bounding box") u koji stanu svi zacrnjeni kvadratići ima stranice  i
i  .
.
Opseg definirajmo kao broj stranica koje ne graniče ni s kojom drugom stranicom.
definirajmo kao broj stranica koje ne graniče ni s kojom drugom stranicom.
U svakom stupcu najmanjeg pravokutnika sa stranicama i
i  ima najmanje
ima najmanje  takve stranice (gornja stranica najgornjeg i donja stranica najdonjeg kvadratića). Analogno vrijedi i za stupce. Iz toga zaključujemo
takve stranice (gornja stranica najgornjeg i donja stranica najdonjeg kvadratića). Analogno vrijedi i za stupce. Iz toga zaključujemo 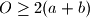 .
.
Također znamo da najmanji pravokutnik mora imati površinu barem (jer sadrži sve kvadratiće). Iz toga dobivamo
(jer sadrži sve kvadratiće). Iz toga dobivamo 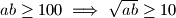 .
.
Sada primjenom nejednakosti dobivamo:
nejednakosti dobivamo: 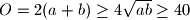 . Jednakost se postiže za
. Jednakost se postiže za 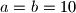 , tj. zacrnjeni kvadrat sa stranicom
, tj. zacrnjeni kvadrat sa stranicom  .
.
 i
i  .
.Opseg
 definirajmo kao broj stranica koje ne graniče ni s kojom drugom stranicom.
definirajmo kao broj stranica koje ne graniče ni s kojom drugom stranicom.U svakom stupcu najmanjeg pravokutnika sa stranicama
 i
i  ima najmanje
ima najmanje  takve stranice (gornja stranica najgornjeg i donja stranica najdonjeg kvadratića). Analogno vrijedi i za stupce. Iz toga zaključujemo
takve stranice (gornja stranica najgornjeg i donja stranica najdonjeg kvadratića). Analogno vrijedi i za stupce. Iz toga zaključujemo 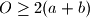 .
.Također znamo da najmanji pravokutnik mora imati površinu barem
 (jer sadrži sve kvadratiće). Iz toga dobivamo
(jer sadrži sve kvadratiće). Iz toga dobivamo 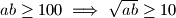 .
.Sada primjenom
 nejednakosti dobivamo:
nejednakosti dobivamo: 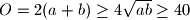 . Jednakost se postiže za
. Jednakost se postiže za 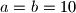 , tj. zacrnjeni kvadrat sa stranicom
, tj. zacrnjeni kvadrat sa stranicom  .
.  Školjka
Školjka