Točno
22. travnja 2012. 18:04 (13 godine, 10 mjeseci)
Za pozitivne brojeve

,

,

,

,

označimo
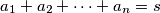
. Dokažite nejednakost
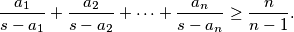
%V0
Za pozitivne brojeve $a_1$, $a_2$, $\dots$, $a_n$, $n \geq 2$ označimo $a_1 + a_2 + \dots + a_n = s$. Dokažite nejednakost
$$\dfrac{a_1}{s - a_1} + \dfrac{a_2}{s - a_2} + \dots + \dfrac{a_n}{s - a_n} \geq \dfrac{n}{n - 1}\text{.}$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Definirajmo nizove
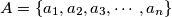
i
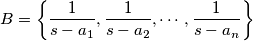
BSOMP
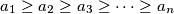
. Onda vrijedi i
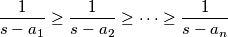
, pa iz MPV nejednakosti slijedi da je
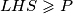
, gdje je P bilo koja premutacija umnožaka
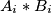
.
Sada vrijedi:
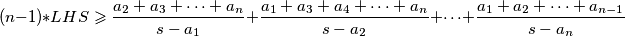
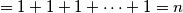
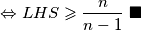
%V0
Definirajmo nizove $A = \left\{ a_1, a_2, a_3, \cdots, a_n \right\}$ i $B = \left\{\dfrac{1}{s-a_1}, \dfrac{1}{s-a_2}, \cdots, \dfrac{1}{s-a_n}\right\}$
BSOMP $a_1 \geq a_2 \geq a_3 \geq \cdots \geq a_n$. Onda vrijedi i $\dfrac{1}{s-a_1} \geq \dfrac{1}{s-a_2} \geq \cdots \geq \dfrac{1}{s-a_n}$, pa iz MPV nejednakosti slijedi da je $ LHS \geqslant P $, gdje je P bilo koja premutacija umnožaka $A_i*B_i$.
Sada vrijedi:
$$(n-1)*LHS \geqslant \frac{a_2+a_3+\cdots+a_n}{s-a_1} + \frac{a_1 + a_3 + a_4 + \cdots + a_n}{s-a_2} + \cdots + \frac{a_1+a_2+\cdots+a_{n-1}}{s-a_n}$$
$$ = 1 + 1 + 1 + \cdots + 1 = n $$
$$\Leftrightarrow LHS \geqslant \frac{n}{n-1}\text{ }\blacksquare$$
| 6. svibnja 2012. 22:34 | ikicic | Točno |
| 22. travnja 2012. 19:04 | grga | Točno |