Točno
22. travnja 2012. 18:08 (12 godine, 7 mjeseci)
Neka su
,
,
pozitivni realni brojevi takvi da je
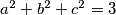
. Dokaži nejednakost
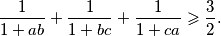
%V0
Neka su $a$, $b$, $c$ pozitivni realni brojevi takvi da je $a^2 + b^2 + c^2 = 3$. Dokaži nejednakost $$\frac{1}{1+ab} + \frac{1}{1+bc} + \frac{1}{1+ca} \geqslant \frac{3}{2} \text{.}$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Iz CSB nejednakosti slijedi:
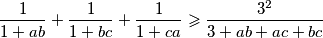
Dok iz MPV nejednakosti imamo
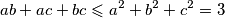
Sada dobivamo
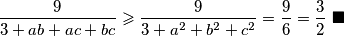
%V0
Iz CSB nejednakosti slijedi:
$$\frac{1}{1+ab} + \frac{1}{1+bc} + \frac{1}{1+ca} \geqslant \frac{3^2}{3 + ab + ac + bc}$$
Dok iz MPV nejednakosti imamo
$$ab+ac+bc \leqslant a^2+b^2+c^2 = 3$$
Sada dobivamo
$$\frac{9}{3+ab+ac+bc} \geqslant \frac{9}{3+a^2+b^2+c^2} = \frac{9}{6} = \frac{3}{2}\text{ }\blacksquare$$
| 22. travnja 2012. 19:04 | grga | Točno |
| 2. svibnja 2012. 20:42 | ikicic | Točno |
Školjka