Točno
22. travnja 2012. 19:06 (13 godine, 10 mjeseci)
U ravnini je dano pet točaka
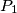
,
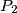
,
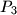
,
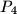
,
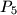
sa cjelobrojnim koordinatama. Pokažite da postoji bar jedan par
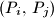
za
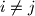
tako da pravac
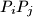
sadrži neku točku

sa cjelobrojnim koordinatama koja leži između
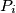
i
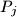
.
%V0
U ravnini je dano pet točaka $P_1$, $P_2$, $P_3$, $P_4$, $P_5$ sa cjelobrojnim koordinatama. Pokažite da postoji bar jedan par $(P_i,\,P_j)$ za $i \neq j$ tako da pravac $P_iP_j$ sadrži neku točku $Q$ sa cjelobrojnim koordinatama koja leži između $P_i$ i $P_j$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Budući da ima pet točaka, a samo četiri različite kombinacije parnosti koordinata točaka, postoje dvije točke takve da su im parnosti koordinata jednake. Nazovimo te točke A i B. Tada su koordinate polovišta dužine AB cijeli brojevi, a polovište leži na pravcu AB između točaka A i B, te je stoga ono jednako traženoj točki Q.
%V0
Budući da ima pet točaka, a samo četiri različite kombinacije parnosti koordinata točaka, postoje dvije točke takve da su im parnosti koordinata jednake. Nazovimo te točke A i B. Tada su koordinate polovišta dužine AB cijeli brojevi, a polovište leži na pravcu AB između točaka A i B, te je stoga ono jednako traženoj točki Q.
| 22. travnja 2012. 19:09 | grga | Točno |
 Školjka
Školjka 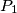 ,
, 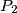 ,
, 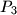 ,
, 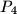 ,
, 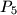 sa cjelobrojnim koordinatama. Pokažite da postoji bar jedan par
sa cjelobrojnim koordinatama. Pokažite da postoji bar jedan par 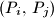 za
za 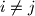 tako da pravac
tako da pravac 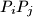 sadrži neku točku
sadrži neku točku  sa cjelobrojnim koordinatama koja leži između
sa cjelobrojnim koordinatama koja leži između 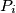 i
i 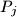 .
.