Točno
22. travnja 2012. 19:28 (13 godine, 10 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Ocjene: (1)
Komentari:
ikicic, 4. svibnja 2012. 15:16
grga, 3. svibnja 2012. 22:21
da znam, netko ga je rjesio preko csba pa sam htio pokazat drugi ( u ovom slucaju opcenitiji ) nacin. dobro ovo dokazivanje konvexnosti je sad malo glupo ispalo jer koristim csb, al ajde.
evo sad mi je pao napamet drukciji nacin
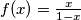 konvexna na intervalu
konvexna na intervalu 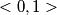 je ekvivalento s tim da je
je ekvivalento s tim da je 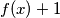 konvexna na tom intervalu, ali
konvexna na tom intervalu, ali 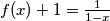 , a to znamo skicirat pa vidimo da je konvexna
, a to znamo skicirat pa vidimo da je konvexna
evo sad mi je pao napamet drukciji nacin
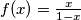 konvexna na intervalu
konvexna na intervalu 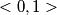 je ekvivalento s tim da je
je ekvivalento s tim da je 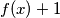 konvexna na tom intervalu, ali
konvexna na tom intervalu, ali 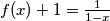 , a to znamo skicirat pa vidimo da je konvexna
, a to znamo skicirat pa vidimo da je konvexna  Školjka
Školjka  ,
,  ,
,  ,
,  ,
,  označimo
označimo 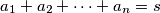 . Dokažite nejednakost
. Dokažite nejednakost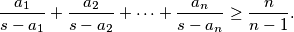
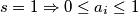 ,
, 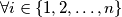
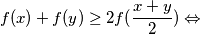
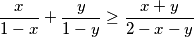 ali kako je po CSB revisited
ali kako je po CSB revisited 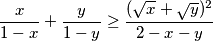
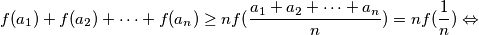
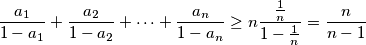
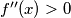 :P
:P