Točno
11. veljače 2014. 20:30 (12 godine, 1 mjesec)
Nađite sve funkcije
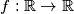
takve da je
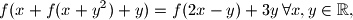
uz uvjet da je

injektivan.
%V0
Nađite sve funkcije $f : \mathbb{R} \rightarrow \mathbb{R}$ takve da je $$f(x+f(x+y^2)+y)=f(2x-y) + 3y \, \forall x, y \in \mathbb{R}\text{,}$$ uz uvjet da je $f$ injektivan.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Uvrstimo
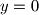
u pocetnu jednadzbu:
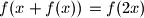
.
Zbog injekcije, slijedi da je
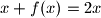
, odnosno
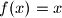
.
No, to rjesenje ne zadovoljava pocetnu jednadzbu. Dakle, ne postoji trazena funkcija.
%V0
Uvrstimo $y = 0$ u pocetnu jednadzbu: $f(x + f(x)) = f(2x)$.
Zbog injekcije, slijedi da je $x + f(x) = 2x$, odnosno $f(x) = x$.
No, to rjesenje ne zadovoljava pocetnu jednadzbu. Dakle, ne postoji trazena funkcija.
| 17. siječnja 2015. 01:26 | grga | Točno |