Točno
22. travnja 2012. 22:20 (13 godine, 10 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
a) Pretpostavimo da 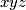 nije djeljiv s
nije djeljiv s  .
.
Tada nijedan od ,
,  ,
,  , nije djeljiv s
, nije djeljiv s  . Kako kvadrati cijelih brojeva
. Kako kvadrati cijelih brojeva 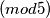 mogu davati samo ostatke
mogu davati samo ostatke 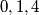 vidimo da
vidimo da  ,
, 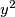 ,
, 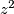 , mogu davati sljedeće uređene trojke ostataka
, mogu davati sljedeće uređene trojke ostataka 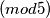 :
: 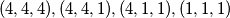 i permutacije. Jasno je da svaki od ovih slučajeva vodi kontradikciji jer nije moguće da svi
i permutacije. Jasno je da svaki od ovih slučajeva vodi kontradikciji jer nije moguće da svi 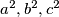 budu potpuni kvadrati jer uvijek neki od njih ne može davati neki od ostataka
budu potpuni kvadrati jer uvijek neki od njih ne može davati neki od ostataka 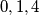
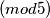 zbog uvjeta zadatka.
zbog uvjeta zadatka.
b)Dovoljno je pokazati djeljivost s . Pretpostavimo da
. Pretpostavimo da 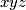 nije djeljiv s
nije djeljiv s  .
.
Tada nijedan od ,
,  ,
,  , nije djeljiv s
, nije djeljiv s  . Kako kvadrati cijelih brojeva
. Kako kvadrati cijelih brojeva 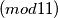 mogu davati samo ostatke
mogu davati samo ostatke 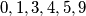 .Vidimo da
.Vidimo da 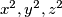 moraju davati neku trojku ostataka iz skupa ostataka
moraju davati neku trojku ostataka iz skupa ostataka 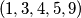 . Vidimo da ako neka dva daju isti ostatak da je to kontradikcija s uvjetom zadatka, dakle svi moraju davati različite ostatke. Sve ostale kombinacije
. Vidimo da ako neka dva daju isti ostatak da je to kontradikcija s uvjetom zadatka, dakle svi moraju davati različite ostatke. Sve ostale kombinacije 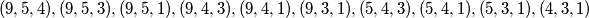 i njihove permutacije daju kontradikciju s uvjetom zadatka.
i njihove permutacije daju kontradikciju s uvjetom zadatka.
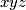 nije djeljiv s
nije djeljiv s  .
. Tada nijedan od
 ,
,  ,
,  , nije djeljiv s
, nije djeljiv s  . Kako kvadrati cijelih brojeva
. Kako kvadrati cijelih brojeva 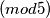 mogu davati samo ostatke
mogu davati samo ostatke 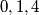 vidimo da
vidimo da  ,
, 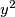 ,
, 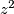 , mogu davati sljedeće uređene trojke ostataka
, mogu davati sljedeće uređene trojke ostataka 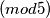 :
: 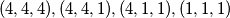 i permutacije. Jasno je da svaki od ovih slučajeva vodi kontradikciji jer nije moguće da svi
i permutacije. Jasno je da svaki od ovih slučajeva vodi kontradikciji jer nije moguće da svi 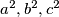 budu potpuni kvadrati jer uvijek neki od njih ne može davati neki od ostataka
budu potpuni kvadrati jer uvijek neki od njih ne može davati neki od ostataka 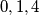
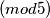 zbog uvjeta zadatka.
zbog uvjeta zadatka.b)Dovoljno je pokazati djeljivost s
 . Pretpostavimo da
. Pretpostavimo da 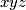 nije djeljiv s
nije djeljiv s  .
. Tada nijedan od
 ,
,  ,
,  , nije djeljiv s
, nije djeljiv s  . Kako kvadrati cijelih brojeva
. Kako kvadrati cijelih brojeva 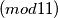 mogu davati samo ostatke
mogu davati samo ostatke 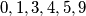 .Vidimo da
.Vidimo da 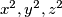 moraju davati neku trojku ostataka iz skupa ostataka
moraju davati neku trojku ostataka iz skupa ostataka 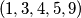 . Vidimo da ako neka dva daju isti ostatak da je to kontradikcija s uvjetom zadatka, dakle svi moraju davati različite ostatke. Sve ostale kombinacije
. Vidimo da ako neka dva daju isti ostatak da je to kontradikcija s uvjetom zadatka, dakle svi moraju davati različite ostatke. Sve ostale kombinacije 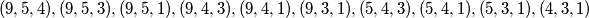 i njihove permutacije daju kontradikciju s uvjetom zadatka.
i njihove permutacije daju kontradikciju s uvjetom zadatka.  Školjka
Školjka 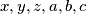 cijeli brojevi za koje vrijedi:
cijeli brojevi za koje vrijedi: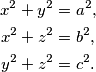 Dokažite da je broj
Dokažite da je broj 

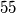 .
.  , ali na kraju sam zaboravio zadnju...; sad je rješeno
, ali na kraju sam zaboravio zadnju...; sad je rješeno kombinacija a trebo bi imat
kombinacija a trebo bi imat 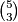
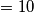 , dakle, neznam koja ti fali al neka ti fali
, dakle, neznam koja ti fali al neka ti fali