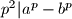Točno
18. svibnja 2014. 09:35 (11 godine, 8 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Podjelimo zadatak na 2 slucaja :
1. slucaj :
p|a i p|b,
onda p^p | a^p i p^p | b^p , pa p^p | a^p - b^p , pa p^2 | a^p - b^p , jer je 2 najmanji prosti broj.
2. slucaj :
p ne dijeli a i p ne dijeli b
Onda mozemo zakljuciti 2 stvari :
1. da je a kongruentno b (mod p) , jer p | a-b , pa moraju oboje davati iste ostatke pri dijeljenu s p
2. da su i a i b relativno prosti s p (jer ako prost broj ne dijeli neki prirodni , oni su relativno prosti)
onda koristimo indentitet :
a^p - b^p = (a-b)( a^(p-1) + a^(p-2)*b + a^(p-3)b^2 ... + b^(p-1))
a-b je po uvjetu zadatka dijeljivo s p , pa ostaje dokazati za drugu zagradu da je dijeliva s p
po malom fermatovom teoremu vrijedi (iz 2. zakljucka) :
a^(p-1) je kongruentno 1 (mod p)
Isto tako iz 1. zakljucka znamo :
a^(p-2)*b kongruento a^(p-1) kongurento 1 (mod p)
Analogno dobijemo za svaki element druge zagrade da daje ostatak jedan s p.
Kako je druga zagrada p-člani skup , zakljucujemo da p dijeli drugu zagradu , pa p^2 dijeli cijeli izraz.
1. slucaj :
p|a i p|b,
onda p^p | a^p i p^p | b^p , pa p^p | a^p - b^p , pa p^2 | a^p - b^p , jer je 2 najmanji prosti broj.
2. slucaj :
p ne dijeli a i p ne dijeli b
Onda mozemo zakljuciti 2 stvari :
1. da je a kongruentno b (mod p) , jer p | a-b , pa moraju oboje davati iste ostatke pri dijeljenu s p
2. da su i a i b relativno prosti s p (jer ako prost broj ne dijeli neki prirodni , oni su relativno prosti)
onda koristimo indentitet :
a^p - b^p = (a-b)( a^(p-1) + a^(p-2)*b + a^(p-3)b^2 ... + b^(p-1))
a-b je po uvjetu zadatka dijeljivo s p , pa ostaje dokazati za drugu zagradu da je dijeliva s p
po malom fermatovom teoremu vrijedi (iz 2. zakljucka) :
a^(p-1) je kongruentno 1 (mod p)
Isto tako iz 1. zakljucka znamo :
a^(p-2)*b kongruento a^(p-1) kongurento 1 (mod p)
Analogno dobijemo za svaki element druge zagrade da daje ostatak jedan s p.
Kako je druga zagrada p-člani skup , zakljucujemo da p dijeli drugu zagradu , pa p^2 dijeli cijeli izraz.
 Školjka
Školjka  vrijedi. Ako
vrijedi. Ako 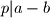 onda
onda