Točno
23. travnja 2012. 00:05 (13 godine, 10 mjeseci)
Neka su

,

i

pozitivni realni brojevi takvi da je
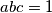
. Dokažite:
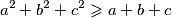
%V0
Neka su $a$, $b$ i $c$ pozitivni realni brojevi takvi da je $abc = 1$. Dokažite:
$$a^2 + b^2 + c^2 \geqslant a + b + c$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
lijevoj strani dodajem
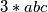
, desnoj

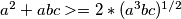
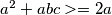
analogno za
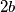
i
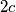
sad treba dokazati
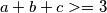
, što se dobiva korištenjem A-G nejednakosti
%V0
lijevoj strani dodajem $3*abc$, desnoj $3$
$a^2+abc>=2*(a^3bc)^{1/2}$
$a^2+abc>=2a$
analogno za $2b$ i $2c$
sad treba dokazati $a+b+c>=3$, što se dobiva korištenjem A-G nejednakosti
| 23. travnja 2012. 00:15 | mimaro | Točno |
| 23. travnja 2012. 00:20 | grga | Točno |