Točno
23. travnja 2012. 12:38 (13 godine, 9 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Neka su brojevi na krugu
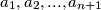
te neka je
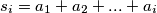
promatrajmo sada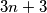 broja
broja 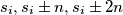 (gdje od tih
(gdje od tih  mogućnosti uzmemo
mogućnosti uzmemo  takve da je broj u intervalu
takve da je broj u intervalu ![[1,3n]](/media/m/9/f/8/9f81341c6861aa85a4dcc180af7516f1.png) ). Primijetimo da ukoliko se neka
). Primijetimo da ukoliko se neka  od tih
od tih 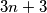 brojeva poklapaju tada imamo neki niz uzastopnih brojeva sa sumom
brojeva poklapaju tada imamo neki niz uzastopnih brojeva sa sumom  ili
ili  . Ako je suma
. Ako je suma  tada svi ostali brojevi imaju sumu
tada svi ostali brojevi imaju sumu  i uzastopni su pa u svakom slučaju imamo traženi niz, a budući da imamo
i uzastopni su pa u svakom slučaju imamo traženi niz, a budući da imamo 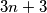 broja, a
broja, a 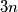 mogućih vrijednosti moramo imati bar dvije iste vrijednosti prema dirichletovom principu.
mogućih vrijednosti moramo imati bar dvije iste vrijednosti prema dirichletovom principu.
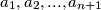
te neka je
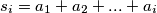
promatrajmo sada
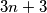 broja
broja 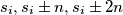 (gdje od tih
(gdje od tih  mogućnosti uzmemo
mogućnosti uzmemo  takve da je broj u intervalu
takve da je broj u intervalu ![[1,3n]](/media/m/9/f/8/9f81341c6861aa85a4dcc180af7516f1.png) ). Primijetimo da ukoliko se neka
). Primijetimo da ukoliko se neka  od tih
od tih 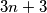 brojeva poklapaju tada imamo neki niz uzastopnih brojeva sa sumom
brojeva poklapaju tada imamo neki niz uzastopnih brojeva sa sumom  ili
ili  . Ako je suma
. Ako je suma  tada svi ostali brojevi imaju sumu
tada svi ostali brojevi imaju sumu  i uzastopni su pa u svakom slučaju imamo traženi niz, a budući da imamo
i uzastopni su pa u svakom slučaju imamo traženi niz, a budući da imamo 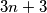 broja, a
broja, a 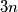 mogućih vrijednosti moramo imati bar dvije iste vrijednosti prema dirichletovom principu.
mogućih vrijednosti moramo imati bar dvije iste vrijednosti prema dirichletovom principu.  Školjka
Školjka  prirodnih brojeva čiji je zbroj
prirodnih brojeva čiji je zbroj  ) čiji je zbroj jednak točno
) čiji je zbroj jednak točno