Magični kvadrat je tablica dimenzija u koju su upisani svi prirodni brojevi od do , na takav način da u svakom stupcu, u svakom retku i na obje dijagonale zbroj upisanih brojeva bude jednak istom broju . Na slici je prikazan jedan magični kvadrat . Odredi zbroj u magičnom kvadratu .
%V0
Magični kvadrat je tablica dimenzija $n \times n$ u koju su upisani svi prirodni brojevi od $1$ do $n^2$, na takav način da u svakom stupcu, u svakom retku i na obje dijagonale zbroj upisanih brojeva bude jednak istom broju $S_n$. Na slici je prikazan jedan magični kvadrat $3 \times 3$.
$4$ $9$ $2$
$3$ $5$ $7$
$8$ $1$ $6$
Odredi zbroj $S_n$ u magičnom kvadratu $n \times n$.
Upozorenje: Ovaj zadatak još niste riješili! Kliknite ovdje kako biste prikazali rješenje.
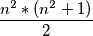
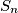
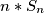
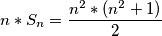
Suma svih brojeva u tablici je . Budući da je suma u svakome retku jednaka , suma svih redaka jednaka je . No to je jednako sumi svih brojeva u tablici, pa vrijedi ,tj. .
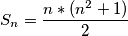
%V0
Suma svih brojeva u tablici je $\dfrac{ n^2*(n^2+1) }{2}$. Budući da je suma u svakome retku jednaka $S_n$, suma svih redaka jednaka je $n*S_n$. No to je jednako sumi svih brojeva u tablici, pa vrijedi $ n*S_n = \dfrac{ n^2*(n^2+1) }{2} $,tj. $S_{n} = \dfrac{n*(n^2+1)}{2}$.
Školjka 
u koju su upisani svi prirodni brojevi od 
do 
, na takav način da u svakom stupcu, u svakom retku i na obje dijagonale zbroj upisanih brojeva bude jednak istom broju 
. Na slici je prikazan jedan magični kvadrat 
.
. Budući da je suma u svakome retku jednaka 
. No to je jednako sumi svih brojeva u tablici, pa vrijedi 
,tj. 
.