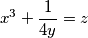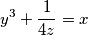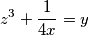Točno
18. svibnja 2014. 10:15 (11 godine, 9 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
promatramo prvu jednadžbu i analogno radimo postupak za ostale :
x^3 + 1 / 4y = z / * 4y
x^3 * 4y + 1 = 4yz
Uvedemo varijable :
4xy = a , 4yz = b , 4zx = c , a iz toga slijedi :
x^2 = a*c/4b
y^2 = a*b/4c
z^2 = b*c/4a
Sustav postaje :
a^2*c/4b + 1 = b (i analogno ostali) , sve mnozimo s 4b (i u ostalim jednadžbama također)
Dobijemo :
a^2*c + 4b = 4b^2
a*b^2 + 4c = 4c^2
b*c^2 + 4a = 4a^2
Primjetimo da ukoliko je jedan od a , b ili c < 0 onda ostali moraju biti > 0.
Uzmemo npr da je a < 0 , a = 4xy , znaci npr x < 0 (za y je analogno).
Znamo : b = 4yz , > 0 , znaci y i z su istog predznaka.
Znamo : c = 4zx > 0 iz cega zakljucujemo da su x i z oboje < 0 , pa to vrijedi i za y , no to je suprotno s pretpostavkom a = 4xy < 0, pa zakljucujemo da su svi > 0.
Sada mozemo uvesti A-G :
a^2*c + 4b >= 4a*sqrt(bc)
a*b^2 + 4c >= 4b*sqrt(ac)
b*c^2 + 4a >= 4c*sqrt(ab)
Sada pomnožimo sve ove nejednakosti , i dobijemo
(a^2*c + 4b)(a*b^2 + 4c)(b*c^2 + 4a) >= 64*a^2*b^2*c^2, što je jednako tome da smo izmnožili dobiveni sustav jednadžbi.
Pa zakljucujemo da jednakost vrijedi samo ako a = b = c = 2 ,
iz čega slijedi da je x = y = z = +- 1 / sqrt(2)
x^3 + 1 / 4y = z / * 4y
x^3 * 4y + 1 = 4yz
Uvedemo varijable :
4xy = a , 4yz = b , 4zx = c , a iz toga slijedi :
x^2 = a*c/4b
y^2 = a*b/4c
z^2 = b*c/4a
Sustav postaje :
a^2*c/4b + 1 = b (i analogno ostali) , sve mnozimo s 4b (i u ostalim jednadžbama također)
Dobijemo :
a^2*c + 4b = 4b^2
a*b^2 + 4c = 4c^2
b*c^2 + 4a = 4a^2
Primjetimo da ukoliko je jedan od a , b ili c < 0 onda ostali moraju biti > 0.
Uzmemo npr da je a < 0 , a = 4xy , znaci npr x < 0 (za y je analogno).
Znamo : b = 4yz , > 0 , znaci y i z su istog predznaka.
Znamo : c = 4zx > 0 iz cega zakljucujemo da su x i z oboje < 0 , pa to vrijedi i za y , no to je suprotno s pretpostavkom a = 4xy < 0, pa zakljucujemo da su svi > 0.
Sada mozemo uvesti A-G :
a^2*c + 4b >= 4a*sqrt(bc)
a*b^2 + 4c >= 4b*sqrt(ac)
b*c^2 + 4a >= 4c*sqrt(ab)
Sada pomnožimo sve ove nejednakosti , i dobijemo
(a^2*c + 4b)(a*b^2 + 4c)(b*c^2 + 4a) >= 64*a^2*b^2*c^2, što je jednako tome da smo izmnožili dobiveni sustav jednadžbi.
Pa zakljucujemo da jednakost vrijedi samo ako a = b = c = 2 ,
iz čega slijedi da je x = y = z = +- 1 / sqrt(2)
Ocjene: (1)
Komentari:
leonstaresinic, 26. svibnja 2014. 14:45
ikicic, 20. svibnja 2014. 20:33
Znamo : b = 4yz , > 0 , znaci y i z su istog predznaka.
trebalo mi je neko vrijeme dok sam shvatio otkud ti ovo slijedi...
cini se ok rjesenje.
Mozes, ako te zanima, pogledati moje rjesenje. Isti princip, samo sto se ranije iskoristi glavni korak.
Zadnja promjena: ikicic, 20. svibnja 2014. 21:28
 Školjka
Školjka  ,
,  ,
,  za koje vrijedi
za koje vrijedi 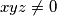 i zadovoljavaju sustav
i zadovoljavaju sustav