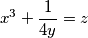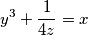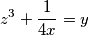Točno
20. svibnja 2014. 20:27 (11 godine, 9 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Promotrimo prvo predznake brojeva  ,
,  i
i  . Ukoliko su svi brojevi negativni, onda zamjenom
. Ukoliko su svi brojevi negativni, onda zamjenom 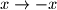 ,
, 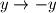 i
i 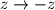 dobivamo ekvivalentnan problem u kojem su
dobivamo ekvivalentnan problem u kojem su  ,
,  i
i  pozitivni. Slučaj jedne negativne i dvije pozitivne varijable nije moguć, jer npr. za
pozitivni. Slučaj jedne negativne i dvije pozitivne varijable nije moguć, jer npr. za 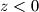 bi se dobila kontradikcija u prvoj jednadžbi. Iz istog razloga ne mogu biti dvije negativne i jedna pozitivna. Dakle, sve su varijable istog predznaka. Pretpostavimo da su pozitivne.
bi se dobila kontradikcija u prvoj jednadžbi. Iz istog razloga ne mogu biti dvije negativne i jedna pozitivna. Dakle, sve su varijable istog predznaka. Pretpostavimo da su pozitivne.
Zbrojimo sada sve jednadžbe: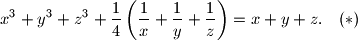 U toj jednadžbi uočavamo tri A-G nejednakosti:
U toj jednadžbi uočavamo tri A-G nejednakosti: 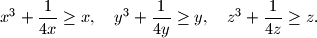
Jednadžba zahtijeva da u svim tim nejednakostima vrijede jednakosti. Dakle,
zahtijeva da u svim tim nejednakostima vrijede jednakosti. Dakle, 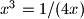 ,
, 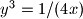 i
i 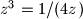 . Budući da su
. Budući da su  ,
,  i
i  istog predznaka, jedina dozvoljena rješenja su:
istog predznaka, jedina dozvoljena rješenja su: 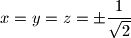
 ,
,  i
i  . Ukoliko su svi brojevi negativni, onda zamjenom
. Ukoliko su svi brojevi negativni, onda zamjenom 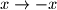 ,
, 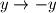 i
i 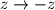 dobivamo ekvivalentnan problem u kojem su
dobivamo ekvivalentnan problem u kojem su  ,
,  i
i  pozitivni. Slučaj jedne negativne i dvije pozitivne varijable nije moguć, jer npr. za
pozitivni. Slučaj jedne negativne i dvije pozitivne varijable nije moguć, jer npr. za 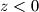 bi se dobila kontradikcija u prvoj jednadžbi. Iz istog razloga ne mogu biti dvije negativne i jedna pozitivna. Dakle, sve su varijable istog predznaka. Pretpostavimo da su pozitivne.
bi se dobila kontradikcija u prvoj jednadžbi. Iz istog razloga ne mogu biti dvije negativne i jedna pozitivna. Dakle, sve su varijable istog predznaka. Pretpostavimo da su pozitivne.Zbrojimo sada sve jednadžbe:
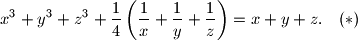 U toj jednadžbi uočavamo tri A-G nejednakosti:
U toj jednadžbi uočavamo tri A-G nejednakosti: 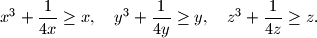
Jednadžba
 zahtijeva da u svim tim nejednakostima vrijede jednakosti. Dakle,
zahtijeva da u svim tim nejednakostima vrijede jednakosti. Dakle, 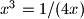 ,
, 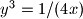 i
i 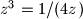 . Budući da su
. Budući da su  ,
,  i
i  istog predznaka, jedina dozvoljena rješenja su:
istog predznaka, jedina dozvoljena rješenja su: 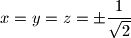
 Školjka
Školjka 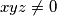 i zadovoljavaju sustav
i zadovoljavaju sustav