Točno
29. svibnja 2014. 19:17 (11 godine, 9 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Primjetimo 2 slucaja , jer je m ocito >= n :
1. n = m
rijesenje je n=m=1
2. m > n
Znaci da je m , minimalno jednako n+1.
Sada zelimo dokazati da za svaki n+1 vrijedi nejednakost (n+1)^n > suma(i^î) do n **
Dokazujemo matematičkom indukcijom :
BAZA : n = 2
(3 ^ 2 = 9) > 5 = (1^1 + 2^2) , znaci vrijedi
PRETPOSTAVKA : ** vrijedi za sve n < k
KORAK : n = k
Po pretpostavci indukcije vrijedi suma k^(k-1) > suma(i^i) do k-1
znaci da je suma(i^i) do k < k^(k-1) + k^k , no to je manje od (k+1)^k .
Po principu matematičke indukcije pretpostavka vrijedi za sve n elemente N. , pa se jednakost u pocetnoj jednadzbi nikada ne postize.
Stoga zakljucujemo n=m=1 je jedino rijesenje.
1. n = m
rijesenje je n=m=1
2. m > n
Znaci da je m , minimalno jednako n+1.
Sada zelimo dokazati da za svaki n+1 vrijedi nejednakost (n+1)^n > suma(i^î) do n **
Dokazujemo matematičkom indukcijom :
BAZA : n = 2
(3 ^ 2 = 9) > 5 = (1^1 + 2^2) , znaci vrijedi
PRETPOSTAVKA : ** vrijedi za sve n < k
KORAK : n = k
Po pretpostavci indukcije vrijedi suma k^(k-1) > suma(i^i) do k-1
znaci da je suma(i^i) do k < k^(k-1) + k^k , no to je manje od (k+1)^k .
Po principu matematičke indukcije pretpostavka vrijedi za sve n elemente N. , pa se jednakost u pocetnoj jednadzbi nikada ne postize.
Stoga zakljucujemo n=m=1 je jedino rijesenje.
 Školjka
Školjka 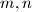 takve da vrijedi:
takve da vrijedi: