Netočno
28. svibnja 2014. 20:53 (11 godine, 9 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Primjetimo da je najveci kvadrat koji mozemo dobiti jednak 15*12*5 ili 12* 10 * 6 = 30^2.
Provjerom svih kvadrata do 30 (uz elemininaciju slucajeva u kojima se radi o kvadratima prostih brojeva i nekih drugih) dobiju se sljedeci skupovi brojeva ciji umnosci daju potpun kvadrat :
(1,2,8) (1,3,12) (1,4,9) (2,3,6) (2,4,8) (2,5,10) (2,6,12) (2,8,9) (3,4,12) (3,6,8) (2,7,14) (3,5,15) (3,9,12) (5,8,10) (12,8,6) (15,10,6) (15,12,5)
Sada se treba odabrati minimalan broj razlicitih brojeva , tako da presjek tog skupa i bilo kojeg od navedenih nije prazan skup.
Primjetimo da se u skupovima najcesce pojavljuju 2 , 3 , 12 i 8.
Razlog zasto je optimalno maknuti npr. 2 umjesto drugih brojeva iz skupova u kojima se on nalazi je taj da bi morali maknuti vise razlicitih brojeva da bi se rijesili svih skupova u kojima se nalazi 2 , sto na kraju dovodi do manjeg rijesenja za velicinu skupa M.
Rijesavanjem slucaja ne stavljanja pojedinog od ovih brojeva u skup M dobije se da M moze imati najvise 10 elemenata , pa zakljucujemo da je 10 rijesenje.
Primjer : {1 , 7 , 8 , 9 ,10 , 11, 12, 13, 14 ,15}
(ako moje rijesnje nije tocno ili ako postoji neko elegantnije molio bih da ga ispravljatelj napise ili da hint za taj nacin rijesavanja , hvala)
Provjerom svih kvadrata do 30 (uz elemininaciju slucajeva u kojima se radi o kvadratima prostih brojeva i nekih drugih) dobiju se sljedeci skupovi brojeva ciji umnosci daju potpun kvadrat :
(1,2,8) (1,3,12) (1,4,9) (2,3,6) (2,4,8) (2,5,10) (2,6,12) (2,8,9) (3,4,12) (3,6,8) (2,7,14) (3,5,15) (3,9,12) (5,8,10) (12,8,6) (15,10,6) (15,12,5)
Sada se treba odabrati minimalan broj razlicitih brojeva , tako da presjek tog skupa i bilo kojeg od navedenih nije prazan skup.
Primjetimo da se u skupovima najcesce pojavljuju 2 , 3 , 12 i 8.
Razlog zasto je optimalno maknuti npr. 2 umjesto drugih brojeva iz skupova u kojima se on nalazi je taj da bi morali maknuti vise razlicitih brojeva da bi se rijesili svih skupova u kojima se nalazi 2 , sto na kraju dovodi do manjeg rijesenja za velicinu skupa M.
Rijesavanjem slucaja ne stavljanja pojedinog od ovih brojeva u skup M dobije se da M moze imati najvise 10 elemenata , pa zakljucujemo da je 10 rijesenje.
Primjer : {1 , 7 , 8 , 9 ,10 , 11, 12, 13, 14 ,15}
(ako moje rijesnje nije tocno ili ako postoji neko elegantnije molio bih da ga ispravljatelj napise ili da hint za taj nacin rijesavanja , hvala)
Ocjene: (1)
Komentari:
grga, 31. kolovoza 2015. 02:03
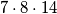 je kvadrat. a i inace,
je kvadrat. a i inace,  je u ovom zadatku "jednak" broju
je u ovom zadatku "jednak" broju  , a i malo je klimavo reci da je nesto "optimalan razlog" bez nekog jakog argumenta.
, a i malo je klimavo reci da je nesto "optimalan razlog" bez nekog jakog argumenta.takoder, fali ti
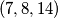 medu onim trojkama.
medu onim trojkama.rjesenje koje imam je daleko od nekog elegantnog i sumnjam da postoji neko super elegantno, ali evo mozda nekad nekom dobro dode:
gledam rastav svakog broja na proste faktore i bitna nam je samo parnost potencije. tj
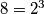 nam igra istu ulogo kao
nam igra istu ulogo kao  .
.zapisimo sada brojeve u tablicu gdje nam
 oznacava neparnu potenciju na doticnom prostom faktoru a
oznacava neparnu potenciju na doticnom prostom faktoru a  parnu
parnu
 i
i  namjerno nisam dodao jer je jasno da njih smijemo "besplatno" dodati u skup
namjerno nisam dodao jer je jasno da njih smijemo "besplatno" dodati u skup  .
.kad sad pogledamo koliko ima kojih uredenih cetvorki dobivamo sljedecu tablicu:
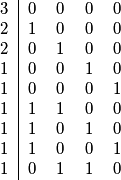
gdje nam sada broj lijevo oznacavo koliko imamo doticnih cetvorki.
dokazat cemo da je max broj elemenata od
 bas
bas  .
. buduci smo rekli da smo
 i
i  vec uzeli, treba odabrati
vec uzeli, treba odabrati  elemenata iz
elemenata iz  .
.zapravo zelimo odabrati neke redove iz tablice tako da ne postoje
 reda koja bi zbrojena po stupcima davala
reda koja bi zbrojena po stupcima davala  (tj "parno") na svakom mjestu.
(tj "parno") na svakom mjestu.to mozemo npr uzimajuci
 elementa
elementa 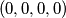 , te
, te  najnizih u tablici.
najnizih u tablici.dokazimo sada da je nemoguce odabrati
 elemenata iz tablice s trazenim svojstvom.
elemenata iz tablice s trazenim svojstvom.  ako ne uzmemo
ako ne uzmemo 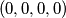 , od preostalih
, od preostalih  moramo uzeti
moramo uzeti  .
.primjetimo da nesmijemo istovremeno uzeti niti
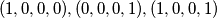 niti
niti 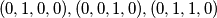 ,
,dakle iz obje trojke moramo izostaviti bar jednoga a kako su trojke disjunktne necemo moci uzeti
 elemenata.
elemenata.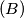 ako uzmemo
ako uzmemo 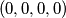 , mozemo "besplatno" uzeti jos jedan takav ali nesmijemo ih uzeti sva tri. takoder,
, mozemo "besplatno" uzeti jos jedan takav ali nesmijemo ih uzeti sva tri. takoder,od preostalih elemenata nesmijemu uzeti nijedan dupli bas jer smo uzeli
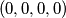 . sada moramo uzeti
. sada moramo uzeti  od
oddonjih
 ali to necemo moci po potpuno istom argumentu kao u prethodnom slucaju.
ali to necemo moci po potpuno istom argumentu kao u prethodnom slucaju.evo, nije posebno elegantno i iskreno ne vjerujem da postoji neki pametan nacin za rjesiti al nadam se da ce nekome pomoci nekada :)
 Školjka
Školjka 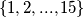 koji ne sadrži
koji ne sadrži