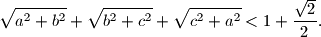Točno
1. lipnja 2014. 12:52 (11 godine, 8 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Uvedimo supstituciju 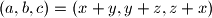 , koju možemo napraviti jer su to stranice trokuta (
, koju možemo napraviti jer su to stranice trokuta ( ,
,  i
i  su duljine dužina između vrhova trokuta i dirališta upisane kružnice).
su duljine dužina između vrhova trokuta i dirališta upisane kružnice).
Zadani uvjet postaje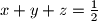 .
.
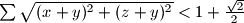
Uzmimo vektore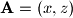 i
i 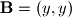 .
.
Po nejednakosti trokuta vrijedi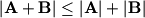 .
.
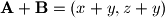
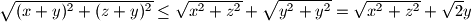
Koristeći trivijalnu nejednakost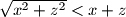 , dobivamo:
, dobivamo:
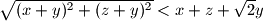
Zbrajajući tri takve nejednakosti, dobivamo:
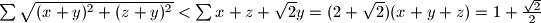

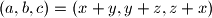 , koju možemo napraviti jer su to stranice trokuta (
, koju možemo napraviti jer su to stranice trokuta ( ,
,  i
i  su duljine dužina između vrhova trokuta i dirališta upisane kružnice).
su duljine dužina između vrhova trokuta i dirališta upisane kružnice).Zadani uvjet postaje
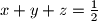 .
.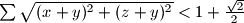
Uzmimo vektore
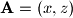 i
i 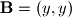 .
.Po nejednakosti trokuta vrijedi
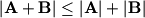 .
.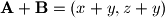
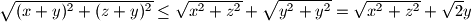
Koristeći trivijalnu nejednakost
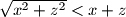 , dobivamo:
, dobivamo: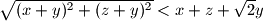
Zbrajajući tri takve nejednakosti, dobivamo:
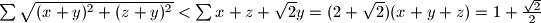

 Školjka
Školjka  ,
,  i
i  duljine stranica trokuta opsega
duljine stranica trokuta opsega  . Dokaži da vrijedi
. Dokaži da vrijedi