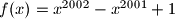
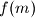
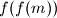
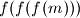
Neka je . Dokazati da su za svaki prirodan broj brojevi , , , , ..., u parovima relativno prosti, tj. da nikoja dva među njima nemaju zajednički djelitelj veći od .
%V0
Neka je $f(x) = x^{2002} - x^{2001} + 1$. Dokazati da su za svaki prirodan broj $m$ brojevi $m$, $f(m)$, $f(f(m))$, $f(f(f(m)))$, ..., u parovima relativno prosti, tj. da nikoja dva među njima nemaju zajednički djelitelj veći od $1$.
Upozorenje: Ovaj zadatak još niste riješili! Kliknite ovdje kako biste prikazali rješenje.
za svaki vrijedi je relativno prost s njime, dakle svi su medjusobno relativno prosti
%V0
$f(ak+b)=(ak+b)^{2002}-(ak+b)^{2001}+1 \equiv b^{2002}-b^{2001}+1 = f(b) \mod a$
$f(1)=1$
$f(f(...(m)...) \equiv f(f(...(0)...) = f(...(1)...) = 1 \mod m$
za svaki $m$ vrijedi $f(...(m)...)$ je relativno prost s njime, dakle svi su medjusobno relativno prosti
Školjka 
. Dokazati da su za svaki prirodan broj 
brojevi 
, 
, 
, ..., u parovima relativno prosti, tj. da nikoja dva među njima nemaju zajednički djelitelj veći od 
. 
je relativno prost s njime, dakle svi su medjusobno relativno prosti