Točno
23. kolovoza 2014. 15:49 (11 godine, 6 mjeseci)
Na istom superultrakul matematičkom kampu, Marko, Petar i Veca igrali su mnogo preferansa. Ako u špilu ima
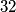
karte, a na početku svatko u ruci ima

karata, koliko ima različitih mogućih početnih kombinacija?
%V0
Na istom superultrakul matematičkom kampu, Marko, Petar i Veca igrali su mnogo preferansa. Ako u špilu ima $32$ karte, a na početku svatko u ruci ima $10$ karata, koliko ima različitih mogućih početnih kombinacija?
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Prvom igracu njegovih

karata mozemo odabrati na
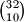
nacina.
Sada nam preostaje jos
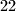
karte, pa drugom igracu njegovih

mozemo podjeliti na
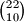
nacina.
Sada od zadnjih

biramo njih

za treceg igraca sto mozemo napraviti na
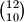
nacina.
Ukupan broj partija je
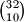
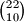
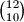
%V0
Prvom igracu njegovih $10$ karata mozemo odabrati na $32 \choose 10$ nacina.
Sada nam preostaje jos $22$ karte, pa drugom igracu njegovih $10$ mozemo podjeliti na $22 \choose 10$ nacina.
Sada od zadnjih $12$ biramo njih $10$ za treceg igraca sto mozemo napraviti na $12 \choose 10$ nacina.
Ukupan broj partija je
$32 \choose 10$ $22 \choose 10$ $12 \choose {10}$
| 23. kolovoza 2014. 15:49 | ikicic | Točno |