Točno
23. srpnja 2014. 02:43 (11 godine, 7 mjeseci)
Sakrij rješenje
Dokaži da u svakom
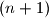
-clanom podskupu skupa
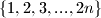
postoje

relativno prosta broja.
%V0
Dokaži da u svakom $(n+1)$-clanom podskupu skupa $\{1,2,3,...,2n\}$ postoje $2$ relativno prosta broja.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Podjelimo skup
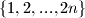
u parove uzastopnih brojeva, tj sparimo

s

,

s

, itd.
Ovakvih parova imamo

pa po Dirichletovom principu da bi odabrali

broj moramo odabrati

iz istog para.
Tada smo odabrali dva broja koji su uzastopni, pa je jasno da su relativno prosti.
%V0
Podjelimo skup $\{1,2,...,2n\}$ u parove uzastopnih brojeva, tj sparimo $1$ s $2$, $3$ s $4$, itd.
Ovakvih parova imamo $n$ pa po Dirichletovom principu da bi odabrali $n+1$ broj moramo odabrati $2$ iz istog para.
Tada smo odabrali dva broja koji su uzastopni, pa je jasno da su relativno prosti.
| 28. srpnja 2014. 17:57 | ikicic | Točno |