Točno
23. srpnja 2014. 02:49 (11 godine, 7 mjeseci)
Sakrij rješenje
Neka je skup

takav da sadrži

cijelih brojeva, i niti jedan element

nije djeljiv s

. Dokaži da je moguće naći podskup od

takav da je suma svih elemenata podskupa djeljiva s

.
%V0
Neka je skup $S$ takav da sadrži $n$ cijelih brojeva, i niti jedan element $S$ nije djeljiv s $n$. Dokaži da je moguće naći podskup od $S$ takav da je suma svih elemenata podskupa djeljiva s $n$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Neka je
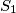
prvi broj.
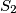
suma prva dva broja
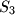
suma prva tri broja.
....
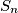
suma svih brojeva.
Ako neka dva
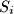
i
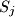
daju isti ostatak pri djeljenju s

, tada je skup elemenata od
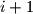
-og do

-tog u sumi djeljiv s

.
Ako niti jedna dva nedaju isti ostatak, onda neki od
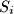
daje ostatak

, pa je on trazeni podskup.
%V0
Neka je $S_1$ prvi broj.
$S_2$ suma prva dva broja
$S_3$ suma prva tri broja.
....
$S_n$ suma svih brojeva.
Ako neka dva $S_i$ i $S_j$ daju isti ostatak pri djeljenju s $n$, tada je skup elemenata od $i+1$-og do $j$-tog u sumi djeljiv s $n$.
Ako niti jedna dva nedaju isti ostatak, onda neki od $S_i$ daje ostatak $0$, pa je on trazeni podskup.
| 28. srpnja 2014. 12:55 | ikicic | Točno |