Točno
23. srpnja 2014. 13:16 (11 godine, 7 mjeseci)
Let

be a set of

residues
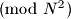
. Prove that there exists a set

of

residues
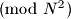
such that
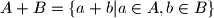
contains at least half of all the residues
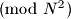
.
%V0
Let $A$ be a set of $N$ residues $\pmod{N^{2}}$. Prove that there exists a set $B$ of $N$ residues $\pmod{N^{2}}$ such that $A + B = \{a+b|a \in A, b \in B\}$ contains at least half of all the residues $\pmod{N^{2}}$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Uzmimo random skup

i označimo

=
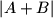
.
Definirajmo
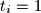
ako
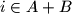
i
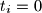
inače. Tada je
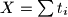
, gdje je suma po svim ostacima modulo
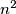
.
Po linearnosti očekivanja vrijedi:
![E[X]=\sum{E[t_i]}=\sum{0 \cdot P[i \notin A+B]+1 \cdot P[i \in A+B]} = \sum{P[i \in A+B]}](/media/m/3/b/a/3bac472dc6074736d60eda603f76cd60.png)
![P[i \in A+B] = P[\exists b \in B, i-b \in A]](/media/m/e/7/9/e79dc340c3bf4919ad58bf699e0520bb.png)
![1-P[i \in A+B] = P[\forall b \in B, i-b \notin A]](/media/m/0/7/f/07fcc5b695bc3a4cd6038f2489d74e02.png)
Gornju vrijednost je lako izračunati; vrijednost

mora izbjegavati onih

ostataka u

pa za to ima
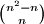
načina, a u nazivniku su svi mogući skupovi

.
![P[\forall b \in B, i-b \notin A] = \frac{\binom{n^2-n}{n}}{\binom{n^2}{n}}](/media/m/f/e/3/fe3f766d7ca3f1d71b41438d6731f30d.png)
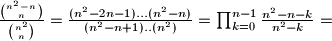
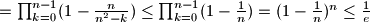
Sada slijedi:
![E[X] = \sum P[i \in A+B] \ge n^2(1-\frac{1}{e}) > \frac{n^2}{2}](/media/m/5/7/8/5787aa8007320ad39fef05b698d1ec22.png)
Sada znamo da postoji
![X \ge E[X] > \frac{n^2}{2}](/media/m/a/f/8/af861015507a418dfe4e69bbab5a300c.png)
, pa postoji

s traženim svojstvom.

%V0
Uzmimo random skup $B$ i označimo $X$ = $|A+B|$.
Definirajmo $t_i=1$ ako $i \in A+B$ i $t_i=0$ inače. Tada je $X=\sum{t_i}$, gdje je suma po svim ostacima modulo $n^2$.
Po linearnosti očekivanja vrijedi:
$E[X]=\sum{E[t_i]}=\sum{0 \cdot P[i \notin A+B]+1 \cdot P[i \in A+B]} = \sum{P[i \in A+B]}$
$P[i \in A+B] = P[\exists b \in B, i-b \in A]$
$1-P[i \in A+B] = P[\forall b \in B, i-b \notin A]$
Gornju vrijednost je lako izračunati; vrijednost $i-b$ mora izbjegavati onih $n$ ostataka u $A$ pa za to ima $\binom{n^2-n}{n}$ načina, a u nazivniku su svi mogući skupovi $B$.
$P[\forall b \in B, i-b \notin A] = \frac{\binom{n^2-n}{n}}{\binom{n^2}{n}}$
$\frac{\binom{n^2-n}{n}}{\binom{n^2}{n}} = \frac{(n^2-2n-1)...(n^2-n)}{(n^2-n+1)..(n^2)} = \prod_{k=0}^{n-1}\frac{n^2-n-k}{n^2-k} =$
$= \prod_{k=0}^{n-1}(1-\frac{n}{n^2-k}) \le \prod_{k=0}^{n-1}(1-\frac{1}{n}) = (1-\frac{1}{n})^n \le \frac{1}{e}$
Sada slijedi:
$E[X] = \sum P[i \in A+B] \ge n^2(1-\frac{1}{e}) > \frac{n^2}{2}$
Sada znamo da postoji $X \ge E[X] > \frac{n^2}{2}$, pa postoji $B$ s traženim svojstvom. $\blacksquare$
| 16. kolovoza 2014. 15:08 | abeker | Točno |
 i označimo
i označimo  =
= 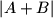 .
.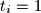 ako
ako 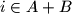 i
i 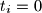 inače. Tada je
inače. Tada je 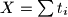 , gdje je suma po svim ostacima modulo
, gdje je suma po svim ostacima modulo 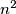 .
.![E[X]=\sum{E[t_i]}=\sum{0 \cdot P[i \notin A+B]+1 \cdot P[i \in A+B]} = \sum{P[i \in A+B]}](/media/m/3/b/a/3bac472dc6074736d60eda603f76cd60.png)
![P[i \in A+B] = P[\exists b \in B, i-b \in A]](/media/m/e/7/9/e79dc340c3bf4919ad58bf699e0520bb.png)
![1-P[i \in A+B] = P[\forall b \in B, i-b \notin A]](/media/m/0/7/f/07fcc5b695bc3a4cd6038f2489d74e02.png)
 mora izbjegavati onih
mora izbjegavati onih  ostataka u
ostataka u  pa za to ima
pa za to ima 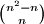 načina, a u nazivniku su svi mogući skupovi
načina, a u nazivniku su svi mogući skupovi  .
.![P[\forall b \in B, i-b \notin A] = \frac{\binom{n^2-n}{n}}{\binom{n^2}{n}}](/media/m/f/e/3/fe3f766d7ca3f1d71b41438d6731f30d.png)
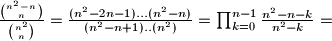
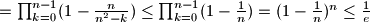
![E[X] = \sum P[i \in A+B] \ge n^2(1-\frac{1}{e}) > \frac{n^2}{2}](/media/m/5/7/8/5787aa8007320ad39fef05b698d1ec22.png)
![X \ge E[X] > \frac{n^2}{2}](/media/m/a/f/8/af861015507a418dfe4e69bbab5a300c.png) , pa postoji
, pa postoji  s traženim svojstvom.
s traženim svojstvom. 
 i označimo
i označimo  =
= 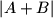 .
.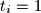 ako
ako 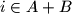 i
i 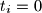 inače. Tada je
inače. Tada je 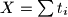 , gdje je suma po svim ostacima modulo
, gdje je suma po svim ostacima modulo 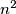 .
.![E[X]=\sum{E[t_i]}=\sum{0 \cdot P[i \notin A+B]+1 \cdot P[i \in A+B]} = \sum{P[i \in A+B]}](/media/m/3/b/a/3bac472dc6074736d60eda603f76cd60.png)
![P[i \in A+B] = P[\exists b \in B, i-b \in A]](/media/m/e/7/9/e79dc340c3bf4919ad58bf699e0520bb.png)
![1-P[i \in A+B] = P[\forall b \in B, i-b \notin A]](/media/m/0/7/f/07fcc5b695bc3a4cd6038f2489d74e02.png)
 mora izbjegavati onih
mora izbjegavati onih  ostataka u
ostataka u  pa za to ima
pa za to ima 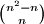 načina, a u nazivniku su svi mogući skupovi
načina, a u nazivniku su svi mogući skupovi  .
.![P[\forall b \in B, i-b \notin A] = \frac{\binom{n^2-n}{n}}{\binom{n^2}{n}}](/media/m/f/e/3/fe3f766d7ca3f1d71b41438d6731f30d.png)
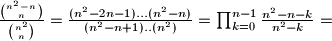
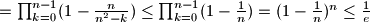
![E[X] = \sum P[i \in A+B] \ge n^2(1-\frac{1}{e}) > \frac{n^2}{2}](/media/m/5/7/8/5787aa8007320ad39fef05b698d1ec22.png)
![X \ge E[X] > \frac{n^2}{2}](/media/m/a/f/8/af861015507a418dfe4e69bbab5a300c.png) , pa postoji
, pa postoji  s traženim svojstvom.
s traženim svojstvom. 
 Školjka
Školjka  residues
residues 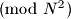 . Prove that there exists a set
. Prove that there exists a set 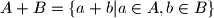 contains at least half of all the residues
contains at least half of all the residues