Točno
26. srpnja 2014. 00:04 (11 godine, 7 mjeseci)
Sakrij rješenje
Dokaži da je skup
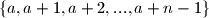
potpuni sustav ostataka modulo

.
%V0
Dokaži da je skup $\{a,a+1,a+2,...,a+n-1\}$ potpuni sustav ostataka modulo $n$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Primjetimo da skup ima tocno

elemenata. Dakle, dozati da svaka dva daju razlicit ostatak pri djeljenju s

.
Pretpostavimo da je
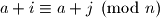
tada
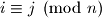
, a kako su i

i

manji od

, imamo
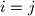
Dakle, svaka dva elementa skupa daju razlicit ostatak modulo

, a kako ih je ukupno

, radi se o potpuno sustavu ostataka.
%V0
Primjetimo da skup ima tocno $n$ elemenata. Dakle, dozati da svaka dva daju razlicit ostatak pri djeljenju s $n$.
Pretpostavimo da je $a+ i \equiv a+j \pmod n$ tada $i \equiv j \pmod n$, a kako su i $i$ i $j$ manji od $n$, imamo $i=j$
Dakle, svaka dva elementa skupa daju razlicit ostatak modulo $n$, a kako ih je ukupno $n$, radi se o potpuno sustavu ostataka.
| 28. srpnja 2014. 18:57 | ikicic | Točno |