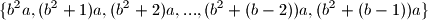
Ako su i relativno prosti prirodni brojevi, pokaži da je potpuni sustav ostataka modulo .
%V0
Ako su $a$ i $b$ relativno prosti prirodni brojevi, pokaži da je $$\{b^2a,(b^2+1)a,(b^2+2)a,...,(b^2+(b-2))a,(b^2+(b-1))a\}$$ potpuni sustav ostataka modulo $b$.
Upozorenje: Ovaj zadatak još niste riješili! Kliknite ovdje kako biste prikazali rješenje.
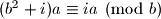
Primjetimo da je Time smo ovo sveli na prosli zadatak.
%V0
Primjetimo da je $(b^2+i)a \equiv ia \pmod b$
Time smo ovo sveli na prosli zadatak.
Školjka 
i 
relativno prosti prirodni brojevi, pokaži da je 
potpuni sustav ostataka modulo 