Točno
26. srpnja 2014. 01:05 (11 godine, 7 mjeseci)
Sakrij rješenje
Dokaži ili opovrgni tvrdnju. Za prost broj

i

relativno prost s

vrijedi da je skup
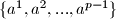
reducirani sustav ostataka modulo

.
%V0
Dokaži ili opovrgni tvrdnju. Za prost broj $p$ i $a$ relativno prost s $p$ vrijedi da je skup $\{a^1,a^ 2,...,a^{p-1}\}$ reducirani sustav ostataka modulo $p$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
To nemora nuzno vrijediti.
Primjerice za
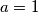
niti za jedan

ovo ne vrijedi.
Ukoliko ovo vrijedi za neki

, tada taj

nazivamo
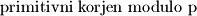
%V0
To nemora nuzno vrijediti.
Primjerice za $a=1$ niti za jedan $p$ ovo ne vrijedi.
Ukoliko ovo vrijedi za neki $a$, tada taj $a$ nazivamo $\text{primitivni korjen modulo p}$
| 28. srpnja 2014. 18:58 | ikicic | Točno |