Točno
26. srpnja 2014. 01:08 (11 godine, 7 mjeseci)
Sakrij rješenje
Dokaži ili opovrgni tvrdnju. Za prost broj

i

relativno prost s

vrijedi da je skup

reducirani sustav ostataka modulo

.
%V0
Dokaži ili opovrgni tvrdnju. Za prost broj $p$ i $a$ relativno prost s $p$ vrijedi da je skup $\{a,2a,3a,...,(p-1)a\}$ reducirani sustav ostataka modulo $p$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Ponovno je dovoljno pokazati da svaka dva elementa daju razlicit ostatak modulo

.
Pretpostavimo da je
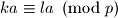
Kako su

i

relativno prosti, mozemo cijelu jednadzbu pomnoziti s inverzom od

.
Tada dobivamo
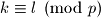
.
Kako su i

i

nuzno manji od

, vrijedi
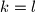
.
Dakle, svi elementi daju razlicite ostatke modulo

.
%V0
Ponovno je dovoljno pokazati da svaka dva elementa daju razlicit ostatak modulo $p$.
Pretpostavimo da je $ka \equiv la \pmod p$
Kako su $a$ i $p$ relativno prosti, mozemo cijelu jednadzbu pomnoziti s inverzom od $a$.
Tada dobivamo $k \equiv l \pmod p$.
Kako su i $k$ i $l$ nuzno manji od $p$, vrijedi $k=l$.
Dakle, svi elementi daju razlicite ostatke modulo $p$.
| 28. srpnja 2014. 18:59 | ikicic | Točno |