Školjka

%V0 eto vidis pametan covjek

%V0 Filip koristi takozvanu metodu elitnog kluba koja u jačim nejednakostima djeluje jako dobro.

%V0 znam znam glupo ali tocno :)

%V0 pa to sam i rekao... samo sam djelio jer sam kreten... jer redim ag na strani koja mi sadrži baš to... ovo kaj si ti napisao je ono što sam ja htio napraviti al se nisam sjetio ovako napisati :)

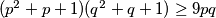
%V0 moram priznat da ja bas nisam shvatio sta zelis reci. malo mi je cudan pocetak tvog razmiljanja. mislim da je zadatak uvjerljivo najlakse rjesiti ovako $(p^2 + p + 1) \geq 3\sqrt[3]{p^2\cdot p\cdot 1} = 3p$, po AGu $(q^2 + q + 1) \geq 3\sqrt[3]{q^2\cdot q\cdot 1} = 3q$, po AGu buduci su obje strane obiju nejednakosti pozitivne, onda ih smijemo pomnoziti pa vrijedi i $(p^2 + p + 1)(q^2 + q + 1) \geq 9pq$