Točno
19. kolovoza 2014. 15:32 (11 godine, 6 mjeseci)
Neka su

,

i

pozitivni realni brojevi. Dokaži da vrijedi
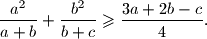
%V0
Neka su $a$, $b$ i $c$ pozitivni realni brojevi. Dokaži da vrijedi $$\frac{a^2}{a+b}+\frac{b^2}{b+c}\geqslant \frac{3a+2b-c}{4}.$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
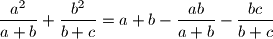
Početna nejednakost postaje
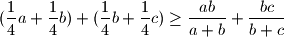
Lako se primjeti da je
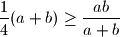
jer je to ekvivalentno redom
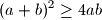
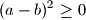
Analogno se pokaže i
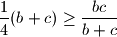
.
Zbrajanjem dobivamo traženu nejednakost.
%V0
$$ \frac{a^2}{a+b} + \frac{b^2}{b+c}= a +b - \frac{ab}{a+b} - \frac{bc}{b+c} $$
Početna nejednakost postaje
$$ (\frac{1}{4}a + \frac{1}{4}b) + (\frac{1}{4}b + \frac{1}{4}c) \geq \frac{ab}{a+b} + \frac{bc}{b+c}$$
Lako se primjeti da je
$$ \frac{1}{4}(a + b) \geq \frac{ab}{a+b} $$
jer je to ekvivalentno redom
$$(a+b)^2 \geq 4ab$$
$$(a-b)^2 \geq 0$$
Analogno se pokaže i
$$\frac{1}{4}(b+c) \geq \frac{bc}{b+c}$$.
Zbrajanjem dobivamo traženu nejednakost.
| 20. kolovoza 2014. 12:03 | ikicic | Točno |