Točno
27. kolovoza 2014. 17:43 (11 godine, 5 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Neka je  pozitivan djeljitelj broja
pozitivan djeljitelj broja  ,
, 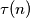 njihov broj i
njihov broj i 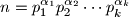 traženi oblik broja
traženi oblik broja  .
.
Poznato je da
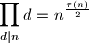
Dokaz:
Promatramo slučajeve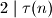 i
i 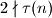
1.slučaj
Svaki djeljitelj broja je oblika
je oblika 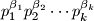 gdje je
gdje je 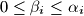 .
.
Dakle ima sveukupno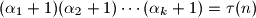 djeljitelja.
djeljitelja.
Zbog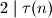 sve djeljitelje možemo grupirati u dvočlane skupove
sve djeljitelje možemo grupirati u dvočlane skupove 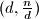 a kako je umnožak
a kako je umnožak 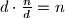 i takvih skupova je
i takvih skupova je 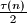 zaključujemo
zaključujemo 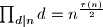
2.slučaj
Analogno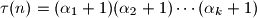 ali zbog
ali zbog 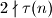 zaključujemo da je
zaključujemo da je  potpuni kvadrat i stoga postoji
potpuni kvadrat i stoga postoji  tako da je
tako da je  . Sve djeljitelje osim toga grupiramo u istih
. Sve djeljitelje osim toga grupiramo u istih 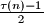 dvočlanih skupova. Na kraju je
dvočlanih skupova. Na kraju je 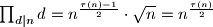
Iz uvjeta zadatka onda redom slijedi
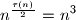
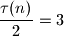
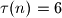
Također znamo da je
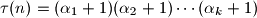 ali
ali 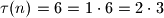
Zaključujemo da je ili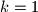 ili
ili 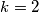 .
.
U prvom slučaju imamo
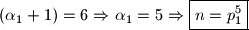
a u drugom na isti način

 pozitivan djeljitelj broja
pozitivan djeljitelj broja  ,
, 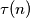 njihov broj i
njihov broj i 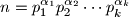 traženi oblik broja
traženi oblik broja  .
.Poznato je da
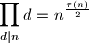
Dokaz:
Promatramo slučajeve
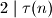 i
i 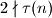
1.slučaj
Svaki djeljitelj broja
 je oblika
je oblika 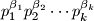 gdje je
gdje je 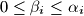 .
.Dakle ima sveukupno
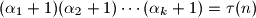 djeljitelja.
djeljitelja.Zbog
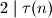 sve djeljitelje možemo grupirati u dvočlane skupove
sve djeljitelje možemo grupirati u dvočlane skupove 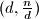 a kako je umnožak
a kako je umnožak 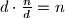 i takvih skupova je
i takvih skupova je 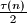 zaključujemo
zaključujemo 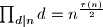
2.slučaj
Analogno
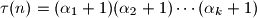 ali zbog
ali zbog 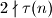 zaključujemo da je
zaključujemo da je  potpuni kvadrat i stoga postoji
potpuni kvadrat i stoga postoji  tako da je
tako da je  . Sve djeljitelje osim toga grupiramo u istih
. Sve djeljitelje osim toga grupiramo u istih 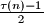 dvočlanih skupova. Na kraju je
dvočlanih skupova. Na kraju je 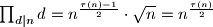
Iz uvjeta zadatka onda redom slijedi
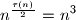
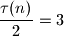
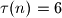
Također znamo da je
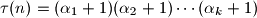 ali
ali 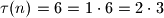
Zaključujemo da je ili
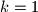 ili
ili 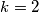 .
.U prvom slučaju imamo
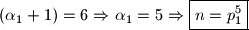
a u drugom na isti način

Ocjene: (1)
Komentari:
ikicic, 27. kolovoza 2014. 13:52
 Školjka
Školjka 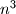 .
.