Točno
29. kolovoza 2014. 14:49 (11 godine, 5 mjeseci)
Odredi formulu za zbroj
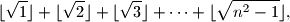
gdje je
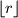
najveći cijeli broj koji nije veći od

.
%V0
Odredi formulu za zbroj $$\lfloor \sqrt{1} \rfloor + \lfloor \sqrt{2} \rfloor + \lfloor \sqrt{3} \rfloor + \cdots + \lfloor\sqrt{n^2-1}\rfloor \text{,}
$$ gdje je $\lfloor r \rfloor$ najveći cijeli broj koji nije veći od $r$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
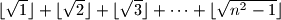
Označimo ovu sumu sa

.
Koristimo se s tvrdnjom
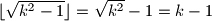
i
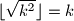
Sada raspišemo nekoliko prvih pribrojnika

i koristimo se sa tvrdnjom da dobijemo:
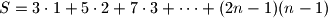
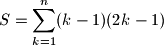
Pri sređivanju ovog izraza se koristimo formulama za zbroj prvih

brojeva (odnosno kvadrata) i dobivamo
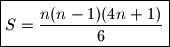
%V0
$\lfloor \sqrt{1} \rfloor + \lfloor \sqrt{2} \rfloor + \lfloor \sqrt{3} \rfloor + \cdots + \lfloor\sqrt{n^2-1}\rfloor$
Označimo ovu sumu sa $S$.
Koristimo se s tvrdnjom $ \lfloor\sqrt{k^2-1}\rfloor = \sqrt{k^2} - 1 = k- 1$ i $ \lfloor \sqrt{k^2} \rfloor = k $
Sada raspišemo nekoliko prvih pribrojnika $S$ i koristimo se sa tvrdnjom da dobijemo:
$$S= 3 \cdot 1 + 5 \cdot 2 + 7 \cdot 3 + \cdots + (2n-1)(n-1)$$
$$S= \sum_{k=1}^n(k-1)(2k-1)$$
Pri sređivanju ovog izraza se koristimo formulama za zbroj prvih $n$ brojeva (odnosno kvadrata) i dobivamo
$$\boxed{S= \dfrac{n(n-1)(4n+1)}{6}}$$
| 29. kolovoza 2014. 15:11 | ikicic | Točno |