Točno
28. travnja 2012. 17:40 (13 godine, 9 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Svaki  za koji ovo vrijedi mora imati u svom rastavu na proste faktore sve proste brojeve
za koji ovo vrijedi mora imati u svom rastavu na proste faktore sve proste brojeve 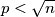 , inače dobivamo
, inače dobivamo 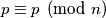 a
a 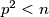 pa
pa 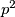 sigurno nije oblike
sigurno nije oblike 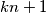 .
.
Pretpostavimo da postoji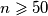 za koji zadatak vrijedi. Tada je
za koji zadatak vrijedi. Tada je 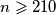 .
.
Kako je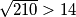 znamo da
znamo da  i
i  dijele
dijele  .
.
Svakim takvim "popravljanjem" (tj dodavanjem novog prostog broja kojeg moramo imati) prelazimo iz u
u 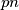 , pa korijen prelazi iz
, pa korijen prelazi iz 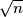 u
u 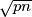
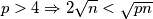 a između
a između 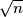 i
i 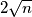 sigurno postoji prost broj pa moramo opet "popravljati".
sigurno postoji prost broj pa moramo opet "popravljati".
Dakle ne postoji veći od 50.
veći od 50.
Za i
i  provjerom dobivamo da vrijedi. Za neparni
provjerom dobivamo da vrijedi. Za neparni 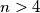 sigurno ne vrijedi, a za
sigurno ne vrijedi, a za 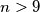 mora biti djeljiv s
mora biti djeljiv s  . Provjerom do 9 dobivamo da vrijedi za
. Provjerom do 9 dobivamo da vrijedi za  ,
, i
i  .
.
Provjerom brojeva ,
,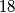 i
i 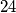 dobivamo da vrijedi za
dobivamo da vrijedi za  i
i 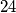 , ali ne i za
, ali ne i za 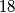 (jer
(jer 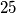 nije kongruentno
nije kongruentno  ).
).
Ako je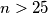 mora biti djeljiv s
mora biti djeljiv s  , a jedini broj manj od
, a jedini broj manj od  i veći od
i veći od 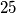 je
je  , za koji ne vrijedi jer
, za koji ne vrijedi jer 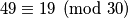 .
.
Dakle jedina rješenja su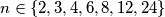
 za koji ovo vrijedi mora imati u svom rastavu na proste faktore sve proste brojeve
za koji ovo vrijedi mora imati u svom rastavu na proste faktore sve proste brojeve 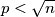 , inače dobivamo
, inače dobivamo 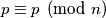 a
a 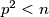 pa
pa 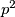 sigurno nije oblike
sigurno nije oblike 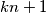 .
.Pretpostavimo da postoji
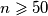 za koji zadatak vrijedi. Tada je
za koji zadatak vrijedi. Tada je 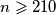 .
.Kako je
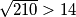 znamo da
znamo da  i
i  dijele
dijele  .
.Svakim takvim "popravljanjem" (tj dodavanjem novog prostog broja kojeg moramo imati) prelazimo iz
 u
u 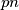 , pa korijen prelazi iz
, pa korijen prelazi iz 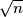 u
u 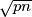
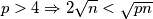 a između
a između 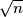 i
i 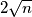 sigurno postoji prost broj pa moramo opet "popravljati".
sigurno postoji prost broj pa moramo opet "popravljati".Dakle ne postoji
 veći od 50.
veći od 50.Za
 i
i  provjerom dobivamo da vrijedi. Za neparni
provjerom dobivamo da vrijedi. Za neparni 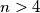 sigurno ne vrijedi, a za
sigurno ne vrijedi, a za 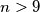 mora biti djeljiv s
mora biti djeljiv s  . Provjerom do 9 dobivamo da vrijedi za
. Provjerom do 9 dobivamo da vrijedi za  ,
, i
i  .
.Provjerom brojeva
 ,
,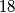 i
i 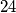 dobivamo da vrijedi za
dobivamo da vrijedi za  i
i 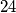 , ali ne i za
, ali ne i za 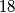 (jer
(jer 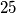 nije kongruentno
nije kongruentno  ).
).Ako je
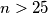 mora biti djeljiv s
mora biti djeljiv s  , a jedini broj manj od
, a jedini broj manj od  i veći od
i veći od 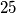 je
je  , za koji ne vrijedi jer
, za koji ne vrijedi jer 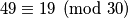 .
.Dakle jedina rješenja su
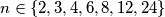
 Školjka
Školjka 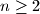 that satisfy the following condition: for all
that satisfy the following condition: for all  and
and  relatively prime to
relatively prime to 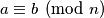 if and only if
if and only if 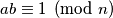 .
.