Točno
3. rujna 2014. 16:20 (11 godine, 5 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Vrijedi: sqrt(k+1) - sqrt(k-1) > 1/sqrt(k), što se lako dokaže kvardiranjem i raspsivanjem.
Takodjer vrijedi 1/sqrt(k) > 2(sqrt(k+1) - sqrt(k)), što se takodjer odmah dokaže raspisivanjem.
Sada imamo nejdnaskost sqrt(k+1) - sqrt(k-1) > 1/sqrt(k) > 2(sqrt(k+1) - sqrt(k)). Sumiranjem za k od 1 do n dobijemo:
sqrt(n+1) + sqrt(n) -1 > 1 + 1/sqrt(2) + ... + 1/sqrt(n) > 2(sqrt(n+1) - 1)
Uvrštavanjem n = 80 konačno se dobiva rješenje (S je suma reciprocnih korijena)
sqrt(81) + sqrt (80) - 1 > S > 2(sqrt(81) - 1) = 2 * (9-1) = 16
17 > 8 + sqrt(80) > S > 16
=====> 17 > S > 16
Takodjer vrijedi 1/sqrt(k) > 2(sqrt(k+1) - sqrt(k)), što se takodjer odmah dokaže raspisivanjem.
Sada imamo nejdnaskost sqrt(k+1) - sqrt(k-1) > 1/sqrt(k) > 2(sqrt(k+1) - sqrt(k)). Sumiranjem za k od 1 do n dobijemo:
sqrt(n+1) + sqrt(n) -1 > 1 + 1/sqrt(2) + ... + 1/sqrt(n) > 2(sqrt(n+1) - 1)
Uvrštavanjem n = 80 konačno se dobiva rješenje (S je suma reciprocnih korijena)
sqrt(81) + sqrt (80) - 1 > S > 2(sqrt(81) - 1) = 2 * (9-1) = 16
17 > 8 + sqrt(80) > S > 16
=====> 17 > S > 16
 Školjka
Školjka 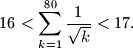
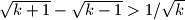 .
.