Točno
5. listopada 2014. 20:18 (10 godine, 1 mjesec)
Prove that the fraction
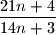
is irreducible for every natural number

.
%V0
Prove that the fraction $\dfrac{21n + 4}{14n + 3}$ is irreducible for every natural number $n$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Suppose the fraction its reducible by factor t where t is an integer.
So that means t | 21n+4 and also t | 14n+3. So t also divides 2*(21n+4)-3*(14n+3)=8-9=-1
So that means t=1 or t=-1. Thus the fraction is irreducible hence we are done.
%V0
Suppose the fraction its reducible by factor t where t is an integer.
So that means t | 21n+4 and also t | 14n+3. So t also divides 2*(21n+4)-3*(14n+3)=8-9=-1
So that means t=1 or t=-1. Thus the fraction is irreducible hence we are done.
| 5. listopada 2014. 21:09 | ikicic | Točno |