Točno
29. travnja 2012. 19:14 (13 godine, 9 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
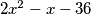 se rastavi kao
se rastavi kao 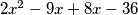 i dalje faktorizira:
i dalje faktorizira: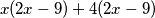
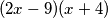
S obzirom na to da je riječ o kvadratu prostog broja, on u rastavu na proste faktore ima samo taj prosti broj i to dvaput, pa nastupaju sljedeći slučajevi:
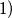
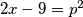
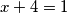
što daje
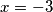 , ali i
, ali i 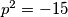 pa rješenja nema
pa rješenja nema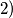
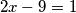
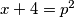
što daje
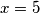 ,
, 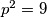 ,
, 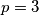
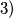
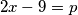
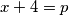
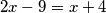
pa se dobiva
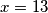 ,
, 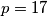
Preostala tri slučaja (za negativne
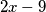 i
i 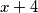 ) ne daju nova rješenja, pa je
) ne daju nova rješenja, pa je 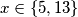
 Školjka
Školjka  je
je 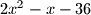 kvadrat prostog broja?
kvadrat prostog broja?