Točno
29. travnja 2012. 22:57 (12 godine, 6 mjeseci)
Za pozitivne brojeve
,
,
,
,
označimo
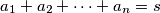
. Dokažite nejednakost
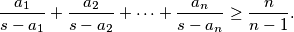
%V0
Za pozitivne brojeve $a_1$, $a_2$, $\dots$, $a_n$, $n \geq 2$ označimo $a_1 + a_2 + \dots + a_n = s$. Dokažite nejednakost
$$\dfrac{a_1}{s - a_1} + \dfrac{a_2}{s - a_2} + \dots + \dfrac{a_n}{s - a_n} \geq \dfrac{n}{n - 1}\text{.}$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
%V0
Zbog $s - a_i > 0$ za svaki $i$ iz Cauchy-Schwarzove nejednakosti slijedi: $$\sum_{i=1}^n \frac{a_i}{s - a_i} = \sum_{i=1}^n \frac{a_i^2}{sa_i - a_i^2} \stackrel{\text{CS}}{\geq} \frac{ \left( \sum a_i \right)^2 }{ s\sum a_i - \sum a_i^2 }$$
Sada imamo:
$$\frac{ \left( \sum a_i \right)^2 }{ s\sum a_i - \sum a_i^2 } \geq \frac{n}{n-1}$$ $$\Updownarrow$$ $$(n-1)s^2 \geq ns^2 - n\sum_{i=1}^n a_i^2$$ $$\Updownarrow$$ $$n\sum_{i=1}^n a_i^2 \geq s^2$$ $$\Updownarrow$$ $$\sqrt{\frac{\sum a_i^2}{n}} \geq \frac{\sum a_i}{n}$$
Dakle, $$\sum_{i=1}^n \frac{a_i}{s - a_i} \geq \frac{n}{n-1}\text{.}$$
| 1. svibnja 2012. 13:07 | mljulj | Točno |
Školjka 
za svaki 
iz Cauchy-Schwarzove nejednakosti slijedi: 
