Točno
5. prosinca 2014. 19:08 (11 godine, 2 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Obzirom da je m? umnožak prvih m prostih brojeva, slijedi da će biti djeljiv s 2 jer je 2 prvi prosti broj. Nakon 2 svi prosti brojevi su neparni (tj. niti jedan neće biti djeljiv s 2), pa slijedi da će m? biti djeljiv s 2, ali ne s 4 ili bilo kojim brojem oblika 2^k gdje je k>1. Kako je n(n+1)(n+2)(n+3) umnožak četiri uzastopna broja, slijedi da će među njima biti barem dva koja su djeljiva s 2 i od kojih je jedan djeljiv s 4 pa vrijedi:
n(n+1)(n+2)(n+3) = 2 * 4 * x = 8 * x. Kako m? nije djeljivo s 8, dolazi do kontradikcije =><=.
n(n+1)(n+2)(n+3) = 2 * 4 * x = 8 * x. Kako m? nije djeljivo s 8, dolazi do kontradikcije =><=.
 Školjka
Školjka  neka je
neka je 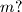 umnožak prvih
umnožak prvih  takvi da je
takvi da je 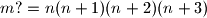 .
.