Netočno
25. siječnja 2015. 11:52 (11 godine, 1 mjesec)
Na stolu se nalaze 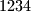 kamenčića. Ratko i Rudi igraju sljedeću igru: najprije Ratko uzme neki paran broj kamenčića, najmanje dva, ali ne više od
kamenčića. Ratko i Rudi igraju sljedeću igru: najprije Ratko uzme neki paran broj kamenčića, najmanje dva, ali ne više od  , a zatim Rudi uzme neki neparan broj kamenčića, najmanje jedan, ali ne više od
, a zatim Rudi uzme neki neparan broj kamenčića, najmanje jedan, ali ne više od 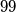 . Potezi se dalje vuku naizmjenično, poštujući iste uvjete. Igrač pobjeđuje ako pokupi sve kamenčiće ili ako drugi igrač ne može odigrati svoj potez. Tko ima pobjedničku strategiju, tj. može pobijediti neovisno o igri drugog igrača?
. Potezi se dalje vuku naizmjenično, poštujući iste uvjete. Igrač pobjeđuje ako pokupi sve kamenčiće ili ako drugi igrač ne može odigrati svoj potez. Tko ima pobjedničku strategiju, tj. može pobijediti neovisno o igri drugog igrača?
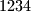 kamenčića. Ratko i Rudi igraju sljedeću igru: najprije Ratko uzme neki paran broj kamenčića, najmanje dva, ali ne više od
kamenčića. Ratko i Rudi igraju sljedeću igru: najprije Ratko uzme neki paran broj kamenčića, najmanje dva, ali ne više od  , a zatim Rudi uzme neki neparan broj kamenčića, najmanje jedan, ali ne više od
, a zatim Rudi uzme neki neparan broj kamenčića, najmanje jedan, ali ne više od 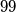 . Potezi se dalje vuku naizmjenično, poštujući iste uvjete. Igrač pobjeđuje ako pokupi sve kamenčiće ili ako drugi igrač ne može odigrati svoj potez. Tko ima pobjedničku strategiju, tj. može pobijediti neovisno o igri drugog igrača?
. Potezi se dalje vuku naizmjenično, poštujući iste uvjete. Igrač pobjeđuje ako pokupi sve kamenčiće ili ako drugi igrač ne može odigrati svoj potez. Tko ima pobjedničku strategiju, tj. može pobijediti neovisno o igri drugog igrača? Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Ovako:
Prema pravilima igre, ako na kraju ostane broj kamencica x, gdje je x e {y|y<100, y=2k-1, k e N}, onda pobjedjuje Rudi (Ako je on na potezu, moze uzeti sve kamencice, ako nije, sto god Ratko napravi, opet on dolazi na potez sa brojem kamencica iz ovog skupa).
Ako je broj kamencica x, gdje je x e {y|y<=100, y=2k, k e N}, onda ako je Ratko na potezu on pobjedjuje, a ako je Rudi na potezu onda on uzme neki broj kamencica i vracamo se na prijasnji slucaj, koji je pobjednicki za Rudija.
Dakle, Rudi pobjedjuje u svim slucajevima kada je manje od 101 kamencica na stolu, osim ako on nije na potezu, a na stolu je paran broj kamencica.
Sada, ako je na stolu broj kamencica izmedju 100 i 200:
Ako je broj kamencica na stolu neparan:
Ako je Rudi na potezu, onda stogod napravi (a da ne da Ratku potez sa parnim brojem kamencica ispod 100), on pobjedjuje, jer stogod Ratko napravi, Rudi ostaje na potezu ili na suprotnoj parnosti iznad 100 (sto cemo dokazati da je pobjednicka), ili ispod 100 uopce sto je pobjednicka situacija
Ako je Ratko na potezu, onda stogod napravi, on gubi, jer onda Rudi dolazi na potez ili na istoj parnosti iznad 100, ili uopce ispod 100
Ako je broj kamencica na stolu paran:
Ako je Ratko na potezu, onda stogod napravi, on gubi jer onda Rudi dolazi na potez ili na istoj parnosti iznad 100, ili uopce ispod 100
Ako je Rudi na potezu onda stogod napravi, on pobjeduje, jer ili ostavlja Ratka na "neparnom" potezu iznad 100, sto je pobjednicka pozicija ili ga ostavlja na neparnom broju kamencica ispod 100 sto je isto pobjednicka pozicija.
Dakle, Rudi uvijek pobjedjuje ako je na stolu manje od 200 kamencica, sto ce se uvijek dogoditi tijekom igre jer nijedan igrac ne moze uzeti vise od 100 kamencica odjednom, sto znaci da ce se uvijek broj kamencica u jednom trenutku igre naci u intervalu [ 100,200 ] .
Prema pravilima igre, ako na kraju ostane broj kamencica x, gdje je x e {y|y<100, y=2k-1, k e N}, onda pobjedjuje Rudi (Ako je on na potezu, moze uzeti sve kamencice, ako nije, sto god Ratko napravi, opet on dolazi na potez sa brojem kamencica iz ovog skupa).
Ako je broj kamencica x, gdje je x e {y|y<=100, y=2k, k e N}, onda ako je Ratko na potezu on pobjedjuje, a ako je Rudi na potezu onda on uzme neki broj kamencica i vracamo se na prijasnji slucaj, koji je pobjednicki za Rudija.
Dakle, Rudi pobjedjuje u svim slucajevima kada je manje od 101 kamencica na stolu, osim ako on nije na potezu, a na stolu je paran broj kamencica.
Sada, ako je na stolu broj kamencica izmedju 100 i 200:
Ako je broj kamencica na stolu neparan:
Ako je Rudi na potezu, onda stogod napravi (a da ne da Ratku potez sa parnim brojem kamencica ispod 100), on pobjedjuje, jer stogod Ratko napravi, Rudi ostaje na potezu ili na suprotnoj parnosti iznad 100 (sto cemo dokazati da je pobjednicka), ili ispod 100 uopce sto je pobjednicka situacija
Ako je Ratko na potezu, onda stogod napravi, on gubi, jer onda Rudi dolazi na potez ili na istoj parnosti iznad 100, ili uopce ispod 100
Ako je broj kamencica na stolu paran:
Ako je Ratko na potezu, onda stogod napravi, on gubi jer onda Rudi dolazi na potez ili na istoj parnosti iznad 100, ili uopce ispod 100
Ako je Rudi na potezu onda stogod napravi, on pobjeduje, jer ili ostavlja Ratka na "neparnom" potezu iznad 100, sto je pobjednicka pozicija ili ga ostavlja na neparnom broju kamencica ispod 100 sto je isto pobjednicka pozicija.
Dakle, Rudi uvijek pobjedjuje ako je na stolu manje od 200 kamencica, sto ce se uvijek dogoditi tijekom igre jer nijedan igrac ne moze uzeti vise od 100 kamencica odjednom, sto znaci da ce se uvijek broj kamencica u jednom trenutku igre naci u intervalu [ 100,200 ] .
Ocjene: (1)
Komentari:
grga, 17. siječnja 2015. 01:23
ovakvo rjesenje ti nije bas dobro. trebas argumentirati sto se desava "u svim mogucim kombinacijama" - naravno, ne mislim da doslovno ispises sve kombinacije, vec da nekako konstruiras argument koji ce opravdavati sve moguce situacije. predlazem da procitas par zadataka iz arhive --> vekijeva vesela vjezbenica -> invarijante
http://www.skoljka.org/folder/533/vekijeva-vesela-vjezbenica/predavanja-za-prve-razrede/invarijante/
http://www.skoljka.org/folder/533/vekijeva-vesela-vjezbenica/predavanja-za-prve-razrede/invarijante/
 Školjka
Školjka