Točno
1. svibnja 2012. 21:11 (12 godine, 7 mjeseci)
Za pozitivne brojeve
,
,
,
,
označimo
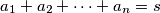
. Dokažite nejednakost
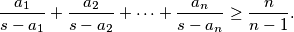
%V0
Za pozitivne brojeve $a_1$, $a_2$, $\dots$, $a_n$, $n \geq 2$ označimo $a_1 + a_2 + \dots + a_n = s$. Dokažite nejednakost
$$\dfrac{a_1}{s - a_1} + \dfrac{a_2}{s - a_2} + \dots + \dfrac{a_n}{s - a_n} \geq \dfrac{n}{n - 1}\text{.}$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Dodamo li svakom izrazu s lijeve strane 1, pribrojnici se transformiraju na sljedeći način:
.
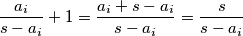
Stoga nejednakost postaje ekvivalentna sljedećoj:
,
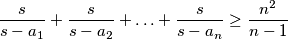
što vrijedi zbog A-H nejednakosti.
%V0
Dodamo li svakom izrazu s lijeve strane 1, pribrojnici se transformiraju na sljedeći način:
$\dfrac{a_i}{s-a_i}+1= \dfrac{a_i + s - a_i}{s - a_i}= \dfrac{s}{s-a_i} $.
Stoga nejednakost postaje ekvivalentna sljedećoj:
$\dfrac{s}{s-a_1} + \dfrac{s}{s-a_2} + \ldots + \dfrac{s}{s-a_n} \geq \dfrac{n^2}{n-1}$,
što vrijedi zbog A-H nejednakosti.
| 1. svibnja 2012. 22:50 | ikicic | Točno |
Školjka