Točno
14. travnja 2012. 16:33 (12 godine, 7 mjeseci)
Odredite sve pozitivne cijele brojeve
za koje jednadžba
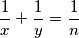
ima točno pet rješenja
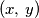
u skupu pozitivnih cijelih brojeva.
%V0
Odredite sve pozitivne cijele brojeve $n$ za koje jednadžba $$\frac1x + \frac1y = \frac1n$$ ima točno pet rješenja $\left(x,\,y\right)$ u skupu pozitivnih cijelih brojeva.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
%V0
$1/x + 1/y = 1/n$
$(x+y)/xy=1/n/ ^-1$
$xy/(x+y)=n /*(x+y)$
$xy=nx+ny /+n^2$
$xy-nx-xy+n^2=n^2$
$(x-n)(y-n)=n^2$
broj rješenja je broj djeljitelja $n^2$
tj. $n^2$ ima 5 djeljitelja----->$n=p1^a1p2^a2...pn^an$----> broj djeljitelja $(a1+1)(a2+1)...(an+1)$ kako je 5 prost broj onda mora biti $a1=4$ -----> $n^2=p^4$---> $n=p^2$
| 14. travnja 2012. 17:46 | grga | Točno |
Školjka 
----> broj djeljitelja 
kako je 5 prost broj onda mora biti 
-----> 
---> 